一般化線形モデル

7.5. 一般化線形モデル#

回帰分析では、目的変数をモデル化した際に生じる誤差が正規分布に従うことを仮定しています。例えば、目的変数 \( Y \) を、説明変数 \( X_{1}, X_{2}, \cdots, X_{n} \) でモデル化したとします。

\[ Y = \beta_{0} + \beta_{1}X_{1} + \beta_{2}X_{2} + \cdots + \beta_{n}X_{n} + \epsilon \]

このとき、誤差項 \(\epsilon\) は正規分布に従う必要があります。もしモデルを評価した際に、誤差項が正規分布から大きく外れている場合は、モデルが妥当でない可能性があります。そのような場合は、誤差の分布の特徴に応じて適切な分布を仮定し解析を行う一般化線形モデル（generalized linear model; GLM）を用いることで、より適切なモデルが得られることが多いです。本節では、この一般化線形モデルについて説明します。

7.5.1. 線形回帰#

一般化線形モデルのうち、誤差項が正規分布に従う場合には、これを回帰分析と呼ぶことがあります。そのため、一般化線形モデルの枠組みを用いて回帰分析を行うことも可能です。哺乳類の睡眠時間のデータを例にとり、睡眠時間（TotalSleep）を使って、寿命（LifeSpan）を説明する回帰モデルを構築してみよう。

まず、データを読み込みます。

# !wget https://py.biopapyrus.jp/data/msleep.txt
msleep = pd.read_csv('msleep.txt', sep='\t', comment='#')
msleep = msleep.dropna()
msleep.head()
Species BodyWt BrainWt NonDreaming Dreaming TotalSleep LifeSpan Gestation Predation Exposure Danger
1 Africangiantpouchedrat 1.000 6.6 6.3 2.0 8.3 4.5 42.0 3 1 3
4 Asianelephant 2547.000 4603.0 2.1 1.8 3.9 69.0 624.0 3 5 4
5 Baboon 10.550 179.5 9.1 0.7 9.8 27.0 180.0 4 4 4
6 Bigbrownbat 0.023 0.3 15.8 3.9 19.7 19.0 35.0 1 1 1
7 Braziliantapir 160.000 169.0 5.2 1.0 6.2 30.4 392.0 4 5 4

次に、statsmodels ライブラリ api モジュールの GLM 関数を用いて回帰分析を行います。この関数は OLS 関数と同様に、目的変数と説明変数を順に引数として渡して使用します。また、モデルに定数項（切片）を含めるため、説明変数にすべての値が 1 の列を追加する必要があります。

import statsmodels.api as sm

y = msleep['LifeSpan']
X = msleep['TotalSleep']

m_lm = sm.GLM(y, sm.add_constant(X))
fit_lm = m_lm.fit()

fit_lm.summary()
Generalized Linear Model Regression Results
Dep. Variable: LifeSpan No. Observations: 42
Model: GLM Df Residuals: 40
Model Family: Gaussian Df Model: 1
Link Function: Identity Scale: 359.09
Method: IRLS Log-Likelihood: -182.13
Date: Tue, 15 Jul 2025 Deviance: 14364.
Time: 10:40:21 Pearson chi2: 1.44e+04
No. Iterations: 3 Pseudo R-squ. (CS): 0.1515
Covariance Type: nonrobust
coef std err z P>|z| [0.025 0.975]
const 36.8795 7.299 5.052 0.000 22.573 51.186
TotalSleep -1.6451 0.628 -2.618 0.009 -2.877 -0.413

推定された回帰直線と実際の観測値をグラフに描き、モデルを可視化してみましょう。

x_ = np.linspace(X.min(), X.max(), 100)
y_ = fit_lm.get_prediction(sm.add_constant(x_))

y_sum = y_.summary_frame(alpha=0.05)


fig = plt.figure()
ax = fig.add_subplot()

# data
ax.scatter(X, y)

# regression line
ax.plot(x_, y_sum['mean'])

# confidence interval
ax.fill_between(x_, y_sum['mean_ci_lower'], y_sum['mean_ci_upper'],
                lw=0, color='#34675c', alpha=0.4, label='CI 95%')

ax.set_xlabel('TotalSleep')
ax.set_ylabel('LifeSpan')
ax.legend()
plt.show()
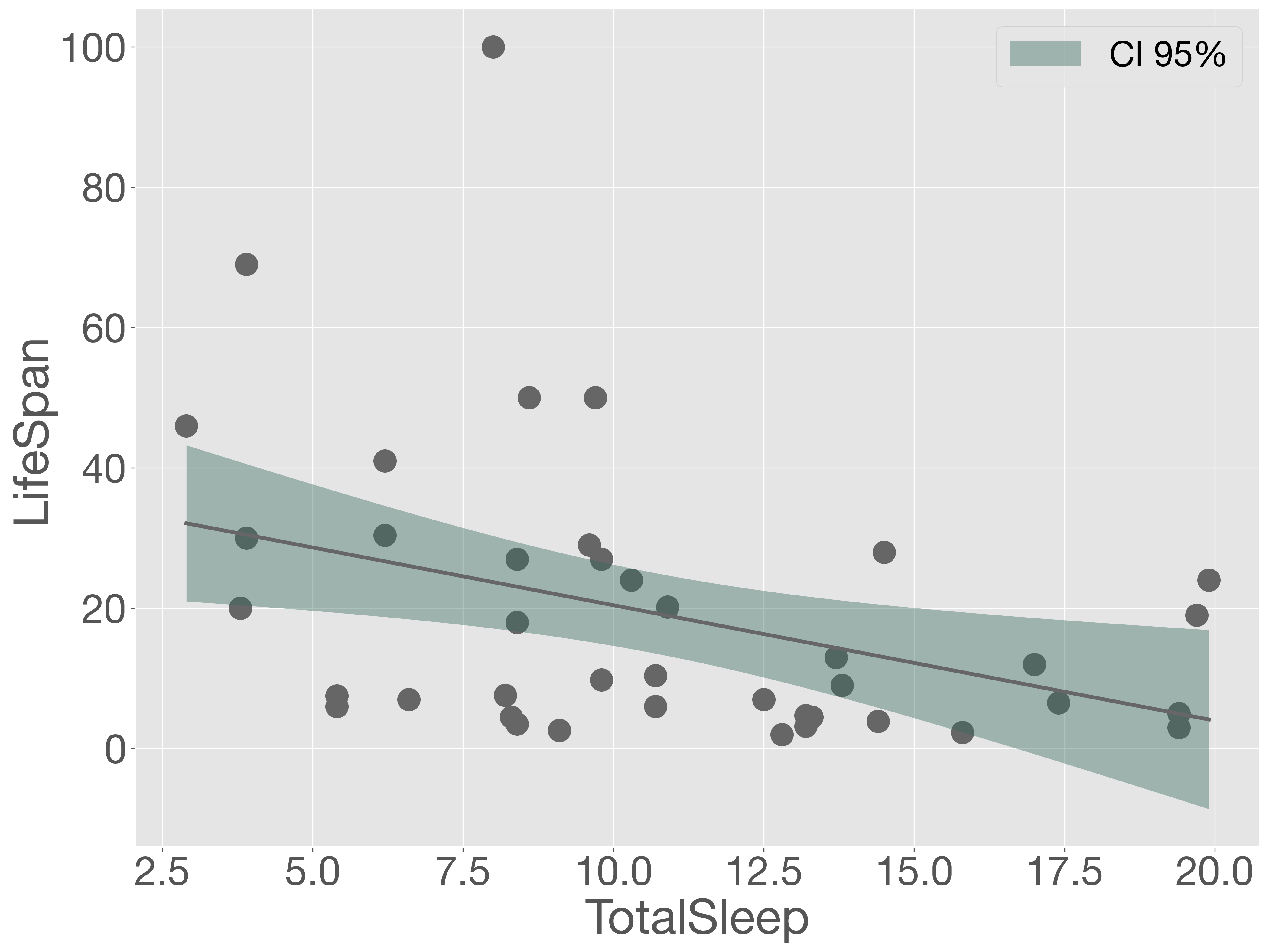
../_images/3540109b00631344300dd31288e881a8b29b6510707e90296d7c183480517162.png

睡眠時間（TotalSleep）の値が小さいほど、誤差が大きくなる傾向が見られます。次に、この誤差の分布を可視化し、詳しく評価していきます。

err = y - fit_lm.predict(sm.add_constant(X))

fig = plt.figure()

ax1 = fig.add_subplot(1, 2, 1)
ax1.plot([X.min(), X.max()], [0, 0])
ax1.vlines(X, 0, err, linestyles='dashed')
ax1.scatter(X, err)
ax1.set_xlabel('TotalSleep')
ax1.set_ylabel('error')

ax2 = fig.add_subplot(1, 2, 2)
ax2.hist(err)

plt.show()
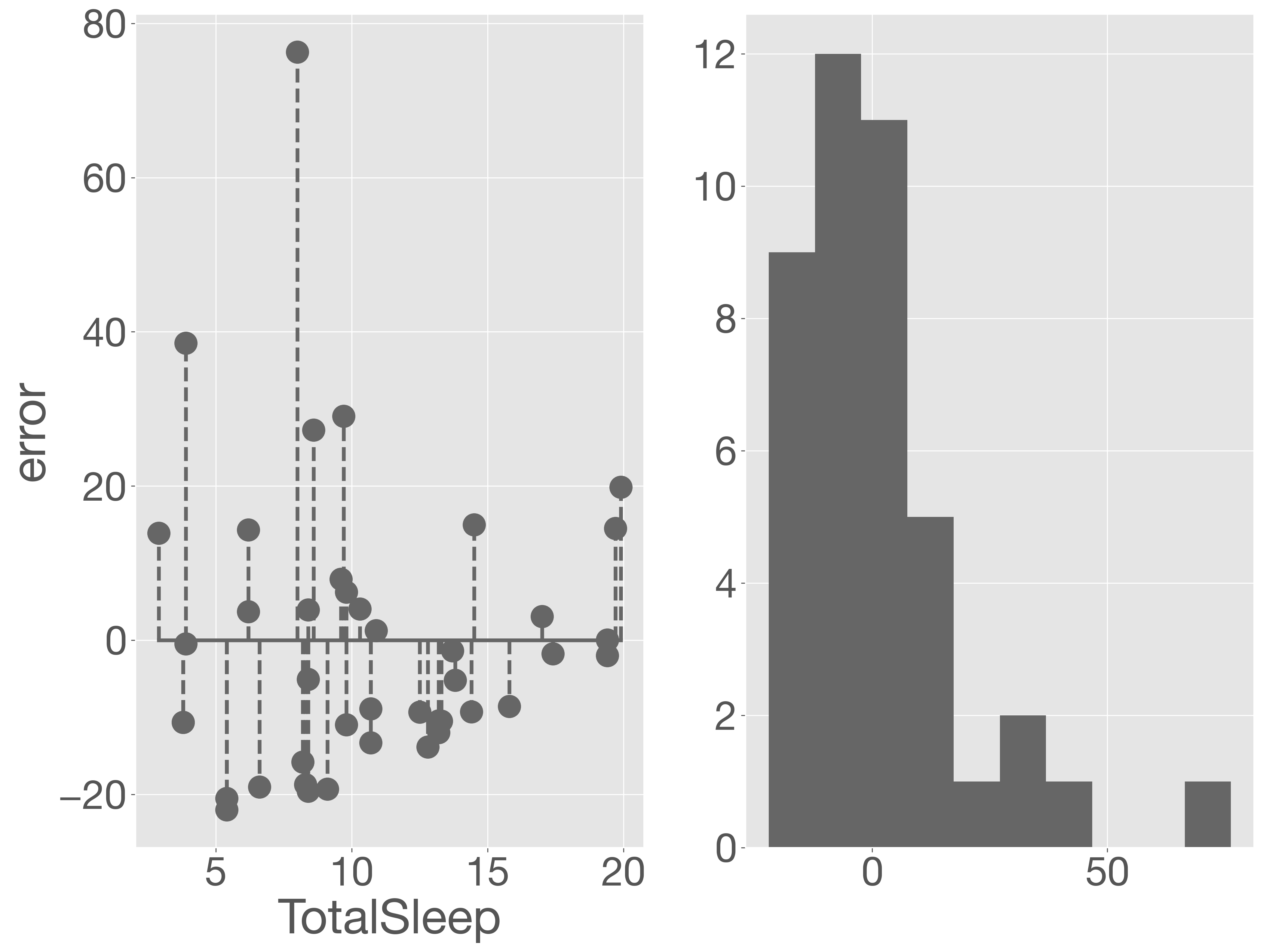
../_images/426e2ad37f58d2b64f43b42144696fffabb10f0359ba53c0872b407a2327f733.png

残差プロットを見ると、睡眠時間（TotalSleep）が短いほど誤差（残差）が大きくなることが確認できます。また、誤差の分布を確認すると、ピークは 0 に近いものの、右側の裾が長くなっており、正規分布からはかけ離れています。つまり、このモデルは妥当とは言いにくい状況です。

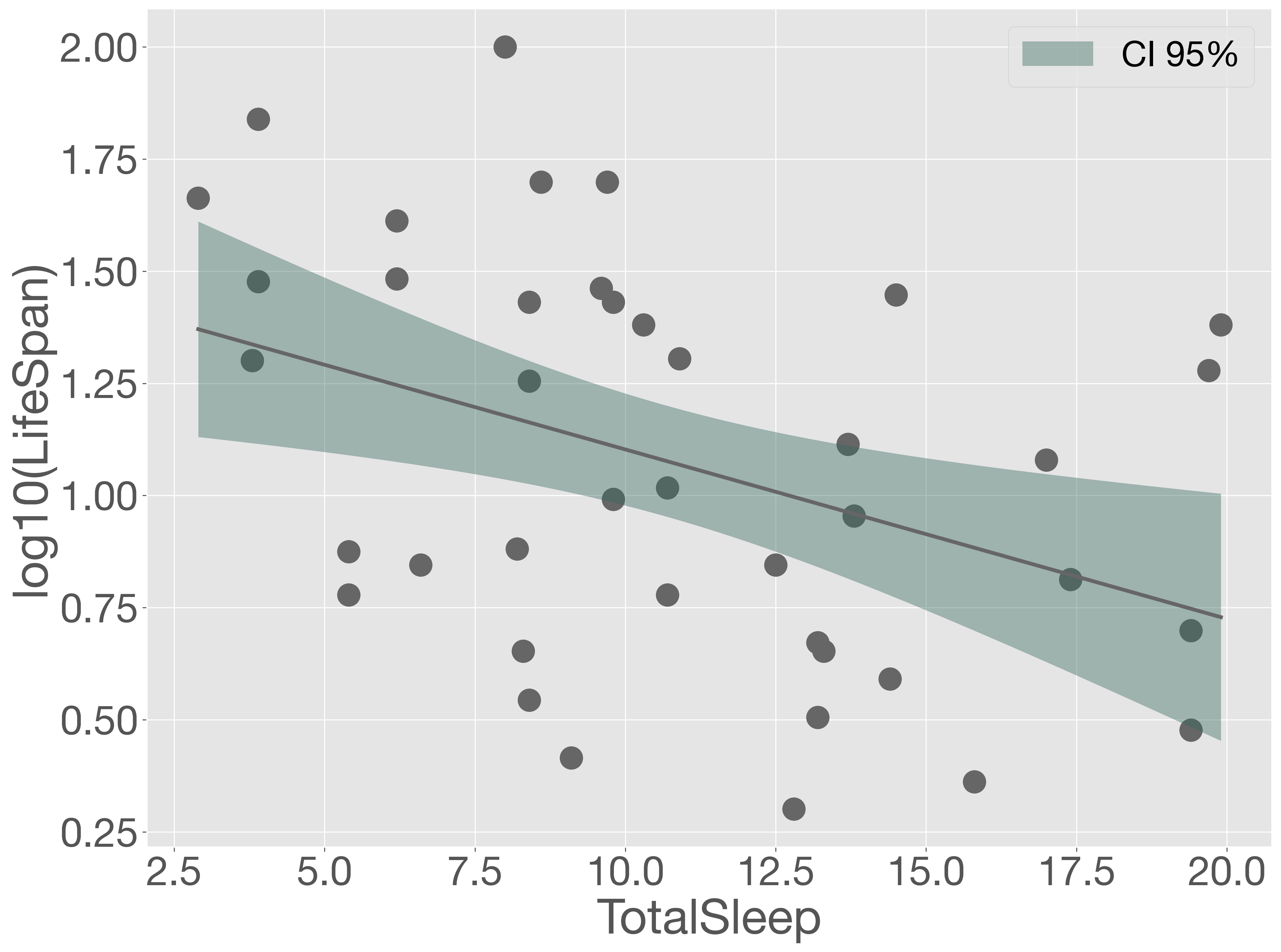
そこで、目的変数を対数変換してスケールを小さくし、再度同様の回帰分析を行ってみます。

y = np.log10(msleep['LifeSpan'])
X = msleep['TotalSleep']

m_loglm = sm.GLM(y, sm.add_constant(X))
fit_loglm = m_loglm.fit()

x_ = np.linspace(X.min(), X.max(), 100)
y_ = fit_loglm.get_prediction(sm.add_constant(x_))

y_sum = y_.summary_frame(alpha=0.05)


fig = plt.figure()
ax = fig.add_subplot()

# data
ax.scatter(X, y)

# regression line
ax.plot(x_, y_sum['mean'])

# confidence interval
ax.fill_between(x_, y_sum['mean_ci_lower'], y_sum['mean_ci_upper'],
                lw=0, color='#34675c', alpha=0.4, label='CI 95%')

ax.set_xlabel('TotalSleep')
ax.set_ylabel('log10(LifeSpan)')
ax.legend()
plt.show()
../_images/c76cd82f23df1df336d090b40b3aa0bfe5fdcb3a66631ba123c5c12130aa8750.png 
err = y - fit_loglm.predict(sm.add_constant(X))

fig = plt.figure()

ax1 = fig.add_subplot(1, 2, 1)
ax1.plot([X.min(), X.max()], [0, 0])
ax1.vlines(X, 0, err, linestyles='dashed')
ax1.scatter(X, err)
ax1.set_xlabel('TotalSleep')
ax1.set_ylabel('error')

ax2 = fig.add_subplot(1, 2, 2)
ax2.hist(err)

plt.show()
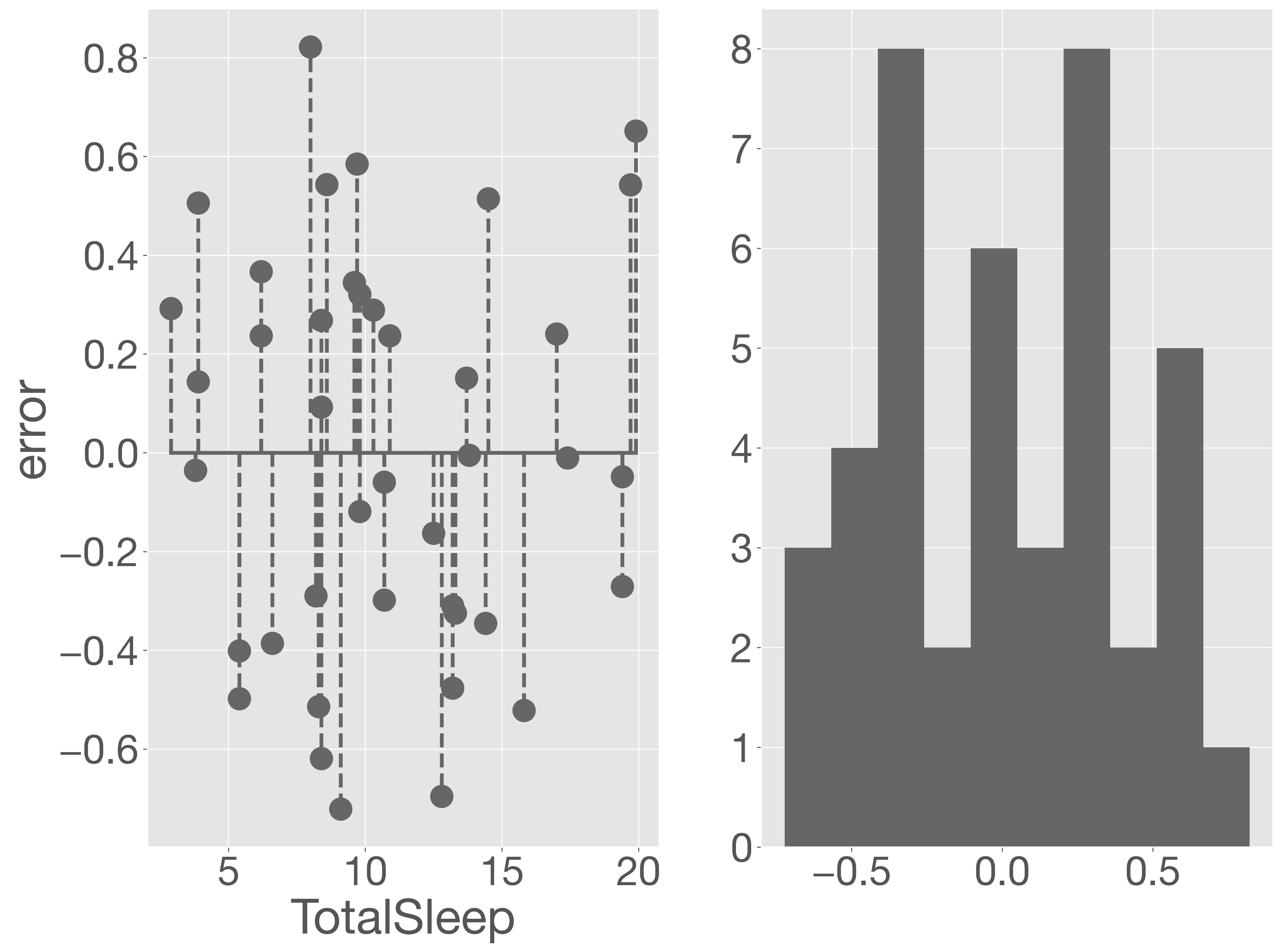
../_images/431df1cc73bd33af720cb7a7fea8f4b4a3f13a973924aaf1e36aa9f104b9296d.png

このように、目的変数を対数化することで、予測誤差が小さくなるだけでなく、誤差項の分布も正規分布に近づいているように見えます。その結果、モデル全体の性能が大きく改善されました。

今回のモデルは、変数変換を行ったうえで回帰分析を実施しているため、次のような式で表されます。

\[ \log \text{LifeSpan} = \beta_{0} + \beta_{1} \text{TotalSleep} \]

この考え方が一般化線形モデルの基本となっています。

7.5.2. 一般化線形モデル#

一般化線形モデル（GLM）は、線形予測子（linear predictor）、リンク関数（link function）、および誤差構造（error structure）の3つの要素から構成されます。線形予測子とは、説明変数と係数の一次結合で表される数式です。たとえば、\(n\) 個の説明変数 \(X_{1}, X_{2}, \cdots, X_{n}\) に対して、

\[ \eta = \beta_{0} + \beta_{1}X_{1} + \beta_{2}X_{2} + \cdots + \beta_{n}X_{n} \]

と表され、この \(\eta\) が線形予測子です。

リンク関数は、目的変数の期待値（平均）と線形予測子を対応付ける関数です。以下のように表されます。

\[ g(\mathbb{E}[Y]) = \eta \]

ここで、\(g\) はリンク関数であり、モデルによって適切な関数が選ばれます。たとえば、ロジスティック回帰ではロジット関数などが選ばれます。

誤差構造とは、目的変数 \(Y\) の確率分布のことです。これは、目的変数のばらつき（分散）をどのようにモデル化するかという重要な要素です。たとえば、目的変数のばらつきが一定（等分散）と考えられる場合には、正規分布が適用され、これは通常の線形回帰に相当します。一方、個体数などの計数データでは、値が大きくなるほど分散も大きくなる傾向があります。このような場合、目的変数はポアソン分布や負の二項分布に従うと仮定し、分散が平均値に比例あるいはより大きくなるような誤差構造を導入します。さらに、目的変数が陽性・陰性などの二値データである場合、目的変数はベルヌーイ分布や二項分布に従うと仮定します。

一般的に、誤差構造を決めると、使用可能なリンク関数も限定されます。以下は、statsmodels ライブラリで指定できる誤差構造とリンク関数の組み合わせです。

誤差構造

リンク関数

Poisson

identity, log, sqrt

Binomial

identity, log, cauchy, logit, probit, cloglog

Gamma

identity, log, inverse_power

Gaussian

identity, log, inverse_power

InverseGaussian

identity, log, inverse_power, inverse_squared

NegativeBinomial

identity, log, cloglog, nbinom, Power

Tweedie

identity, log, Power

7.5.3. ポアソン回帰#

上の例からもわかるように、寿命（LifeSpan）の値が大きくなるほど、そのばらつきも大きくなる傾向が見られます。このように、値が大きくなるにつれてばらつきも増加するようなデータをモデリングする場合には、ポアソン回帰がよく用いられます。ここでは、ポアソン回帰を使って、睡眠時間（TotalSleep）から寿命（LifeSpan）を説明する回帰モデルを構築してみましょう。ポアソン回帰では、リンク関数として対数関数を用いるのが一般的です。

リンク関数が対数関数であるため、概念的には次のような式でモデルが構築されていることになります。

\[ \log Y = \eta = \beta_{0} + \beta_{1}X_{1} + \beta_{2}X_{2} + \cdots + \beta_{n}X_{n} \]

つまり、これは前の例で見たように、目的変数を対数変換してから線形回帰を行っているのとほぼ同じことを意味します。

GLM 関数では、family オプションを使って誤差構造を指定します。また、誤差構造を生成する際に、使用するリンク関数も一緒に指定します。

y = msleep['LifeSpan']
X = msleep['TotalSleep']

link = sm.families.links.Log()
family = sm.families.Poisson(link)

m_poisson = sm.GLM(y, sm.add_constant(X), family=family)
fit_poisson = m_poisson.fit()

fit_poisson.summary()
Generalized Linear Model Regression Results
Dep. Variable: LifeSpan No. Observations: 42
Model: GLM Df Residuals: 40
Model Family: Poisson Df Model: 1
Link Function: Log Scale: 1.0000
Method: IRLS Log-Likelihood: -372.97
Date: Tue, 15 Jul 2025 Deviance: 563.55
Time: 10:40:24 Pearson chi2: 668.
No. Iterations: 5 Pseudo R-squ. (CS): 0.9596
Covariance Type: nonrobust
coef std err z P>|z| [0.025 0.975]
const 3.8694 0.082 47.353 0.000 3.709 4.030
TotalSleep -0.0934 0.008 -11.146 0.000 -0.110 -0.077

次に、観測値に加えて、モデルによる回帰直線、信頼区間、および予測区間を可視化します。なお、GLM 関数で生成されたオブジェクトでは、予測区間を自動的に計算することはできないため、ここでは予測区間と信頼区間を計算する関数をあらかじめ定義しておく必要があります。

from scipy.stats import norm

def summarize_poisson_model(x, model, link):
    x_ = sm.add_constant(x)
    eta = model.predict(x_, linear=True)
    cov = model.cov_params()
    se_eta = np.sqrt(np.sum(x_ @ cov * x_, axis=1))

    z = norm.ppf(0.975)

    # predicted y
    mean_pred = link.inverse(eta)

    # CI
    eta_lw = eta - z * se_eta
    eta_up = eta + z * se_eta
    ci_lw = link.inverse(eta_lw)
    ci_up = link.inverse(eta_up)

    # PI
    var_pred = se_eta**2 + 1 / mean_pred
    pi_lw = np.exp(eta - z * np.sqrt(var_pred))
    pi_up = np.exp(eta + z * np.sqrt(var_pred))

    return pd.DataFrame({'x': x, 'y': mean_pred,
                         'ci_lw': ci_lw, 'ci_up': ci_up,
                         'pi_lw': pi_lw, 'pi_up': pi_up})

この関数を利用して、モデルの可視化を行います。

x_ = np.linspace(X.min(), X.max(), 100)
y_ = summarize_poisson_model(x_, fit_poisson, link)

fig = plt.figure()
ax = fig.add_subplot()

# data
ax.scatter(X, y)

# regression line
ax.plot(y_['x'], y_['y'])

# prediction interval
ax.fill_between(x_, y_['pi_lw'], y_['pi_up'],
                lw=0, color='#426e86', alpha=0.2, label='PI 95%')

# confidence interval
ax.fill_between(x_, y_['ci_lw'], y_['ci_up'],
                lw=0, color='#34675c', alpha=0.4, label='CI 95%')

ax.set_xlabel('TotalSleep')
ax.set_ylabel('LifeSpan')
ax.legend()
plt.show()
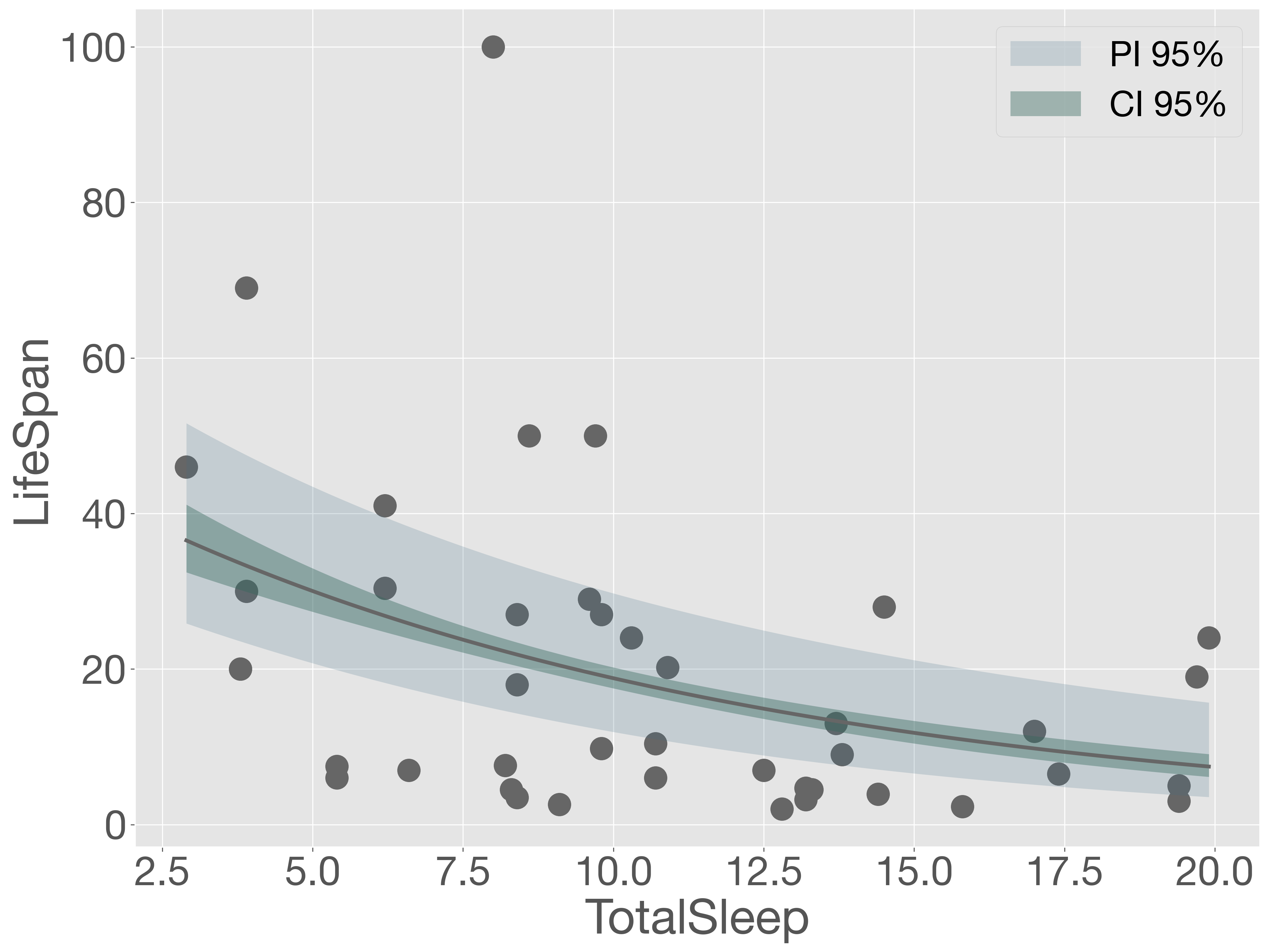
../_images/3a2abdb69d3e4794c3b6a6d9b5e2cc07e2c58c9fc772d2bc2a9f06314876835d.png

このように、ポアソン回帰を行うことで、モデルの予測値は直線的ではなく、目的変数に応じて非線形に変化することがわかります。また、信頼区間および予測区間に注目すると、目的変数の値が大きくなるにつれて、それらの区間も徐々に広がっていることが確認できます。

一方で、予測区間を確認すると、多くの観測点がその範囲の外側に位置していることがわかります。これは、モデルが実際の測定値に対して適切に適合できていないことを示しています。

7.5.4. 負の二項分布回帰#

ポアソン回帰でうまくモデル化できないデータについては、誤差構造を負の二項分布にすることで改善される場合が多くあります。負の二項分布には、大きなばらつき（過分散）を扱える項が含まれており、ポアソン分布より柔軟にデータを表現できます。ただし、この過分散を許容するパラメーター（alpha）は、自動的には推定されません。解析者が事前に値を指定する必要があります。

たとえば、alpha=0.1 を指定してモデルを構築する場合、以下のようにします。

y = msleep['LifeSpan']
X = msleep['TotalSleep']

link = sm.families.links.Log()
family = sm.families.NegativeBinomial(link, alpha=0.1)

m_nb = sm.GLM(y, sm.add_constant(X), family=family)
fit_nb = m_nb.fit()

fit_nb.summary()
Generalized Linear Model Regression Results
Dep. Variable: LifeSpan No. Observations: 42
Model: GLM Df Residuals: 40
Model Family: NegativeBinomial Df Model: 1
Link Function: Log Scale: 1.0000
Method: IRLS Log-Likelihood: -206.21
Date: Tue, 15 Jul 2025 Deviance: 191.70
Time: 10:40:25 Pearson chi2: 226.
No. Iterations: 6 Pseudo R-squ. (CS): 0.6557
Covariance Type: nonrobust
coef std err z P>|z| [0.025 0.975]
const 3.8187 0.150 25.497 0.000 3.525 4.112
TotalSleep -0.0883 0.014 -6.429 0.000 -0.115 -0.061

続いて、モデルを可視化します。ただし、誤差構造にポアソン分布を用いた場合と、負の二項分布を用いた場合とでは、予測区間の計算方法が異なるため、信頼区間および予測区間を算出する関数をあらためて用意する必要があります。

def summarize_nb_model(x, model, link):
    x_ = sm.add_constant(x)
    eta = model.predict(x_, linear=True)
    cov = model.cov_params()
    if cov.shape[0] != x_.shape[1]:
        # object from NegativeBinomial contains estimated 'alpha' 
        cov = cov.iloc[0:-1, 0:-1]
    se_eta = np.sqrt(np.sum(x_ @ cov * x_, axis=1))

    if hasattr(model, 'family') and hasattr(model.family, 'alpha'):
        # object from GLM
        alpha = model.family.alpha
    else:
        # object from NegativeBinomial
        alpha = model.params[-1]

    z = norm.ppf(0.975)

    # predicted y
    mean_pred = link.inverse(eta)
    
    # CI
    eta_lw = eta - z * se_eta
    eta_up = eta + z * se_eta
    ci_lw = link.inverse(eta_lw)
    ci_up = link.inverse(eta_up)
    
    # PI
    var_pred = mean_pred + alpha * mean_pred ** 2
    se_log_pred = np.sqrt(var_pred) / mean_pred
    pred_lw = eta - z * se_log_pred
    pred_up = eta + z * se_log_pred
    pi_lw = link.inverse(pred_lw)
    pi_up = link.inverse(pred_up)

    return pd.DataFrame({
        'x': x,
        'y': mean_pred,
        'ci_lw': ci_lw,
        'ci_up': ci_up,
        'pi_lw': pi_lw,
        'pi_up': pi_up
    })



x_ = np.linspace(X.min(), X.max(), 100)
y_ = summarize_nb_model(x_, fit_nb, link)

fig = plt.figure()
ax = fig.add_subplot()

# data
ax.scatter(X, y)

# regression line
ax.plot(y_['x'], y_['y'])

# prediction interval
ax.fill_between(x_, y_['pi_lw'], y_['pi_up'],
                lw=0, color='#426e86', alpha=0.2, label='PI 95%')

# confidence interval
ax.fill_between(x_, y_['ci_lw'], y_['ci_up'],
                lw=0, color='#34675c', alpha=0.4, label='CI 95%')

ax.set_xlabel('TotalSleep')
ax.set_ylabel('LifeSpan')
ax.legend()
plt.show()
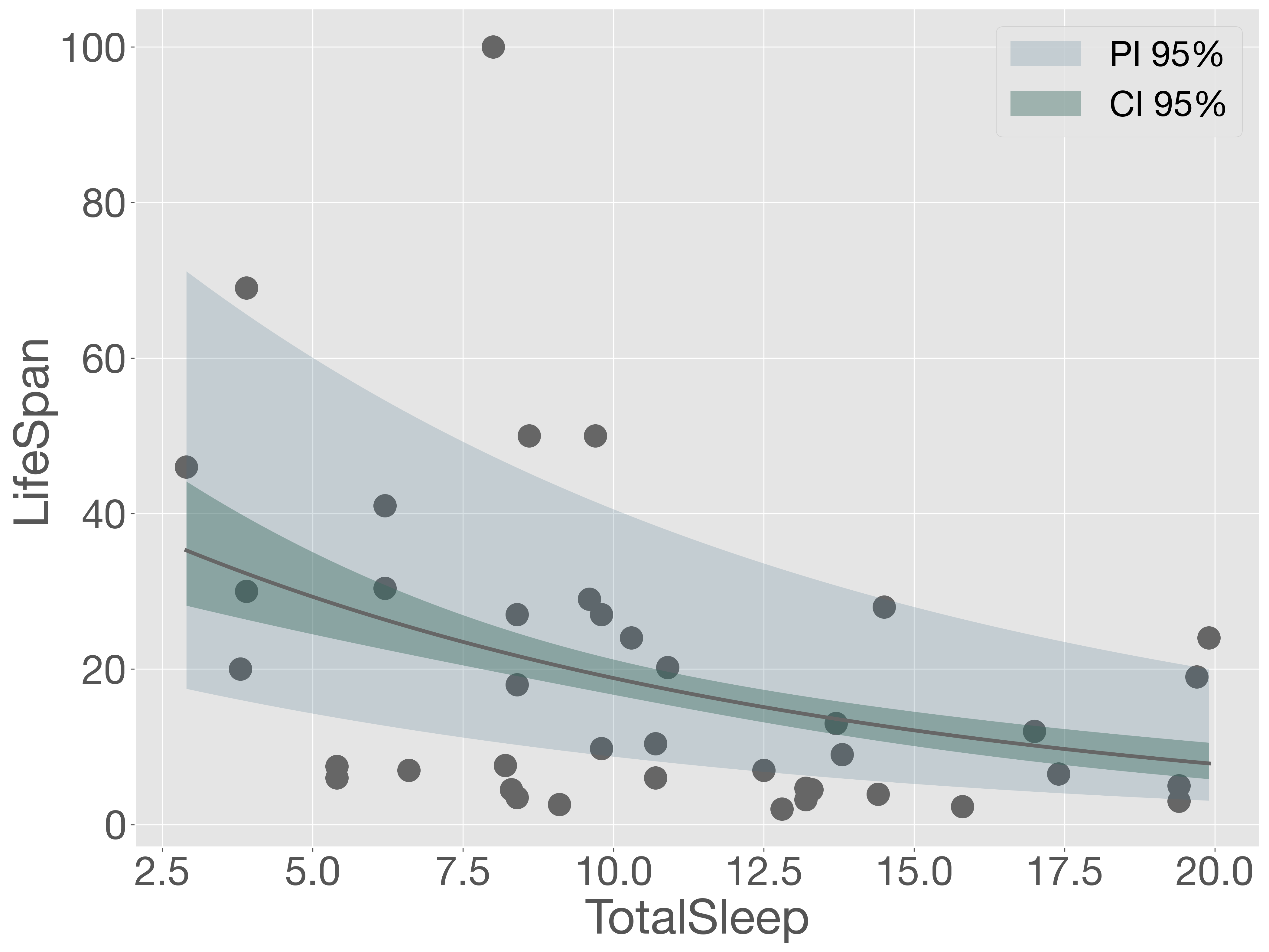
../_images/745b97aae0b43e0af03220954bb002d2e08842e01972f90ffdf5713d14182084.png

予測区間を確認すると、ポアソン回帰と比較して改善は見られるものの、依然として多くの観測値が予測区間の外側にあることがわかります。このことから、モデルにはさらなる改善の余地があると考えられます。

このモデルの AIC は、以下の方法で取得できます。AIC はモデルの適合度を評価する指標で、値が小さいほどモデルの適合度が高く、より適切であることを示します。

fit_nb.aic

np.float64(416.42403252447497)

次に取るべきアプローチとしては、alpha の値を調整して複数のモデルを再構築し、それぞれの AIC を比較することが挙げられます。これにより、AIC が最小となる alpha を見つけ出し、最適なモデルを選択することが可能になります。

練習問題 SGL-1

動物の睡眠時間に関するデータセット msleep.txt を読み込み、睡眠時間（TotalSleep）を用いて寿命（LifeSpan）を説明する回帰モデルを構築しなさい。このとき、誤差構造には負の二項分布を、リンク関数には対数関数を使用してください。また、GLM 関数の alpha パラメーターの値を 0.01、0.1、1、10 に変更しながら分析を行い、それぞれの場合における信頼区間や予測区間の変化について簡単に述べなさい。

GLM 関数では、alpha を解析者が指定する必要がありましたが、statsmodels ライブラリの api モジュールにある NegativeBinomial 関数を使うことで、alpha を自動的に推定することが可能です。以下にその例を示します。

m_nb = sm.NegativeBinomial(y, sm.add_constant(X))
fit_nb = m_nb.fit()
Hide code cell output 
Optimization terminated successfully.
         Current function value: 3.874638
         Iterations: 11
         Function evaluations: 16
         Gradient evaluations: 16

推定結果を確認してみましょう。定数項および説明変数の係数に加え、alpha も 0.6628 と推定されていることが確認できます。

fit_nb.summary()
NegativeBinomial Regression Results
Dep. Variable: LifeSpan No. Observations: 42
Model: NegativeBinomial Df Residuals: 40
Method: MLE Df Model: 1
Date: Tue, 15 Jul 2025 Pseudo R-squ.: 0.02571
Time: 10:40:26 Log-Likelihood: -162.73
converged: True LL-Null: -167.03
Covariance Type: nonrobust LLR p-value: 0.003383
coef std err z P>|z| [0.025 0.975]
const 3.7788 0.309 12.243 0.000 3.174 4.384
TotalSleep -0.0842 0.027 -3.151 0.002 -0.137 -0.032
alpha 0.6628 0.147 4.506 0.000 0.374 0.951

次に、構築したモデルを可視化します。

x_ = np.linspace(X.min(), X.max(), 100)
y_ = summarize_nb_model(x_, fit_nb, link)

fig = plt.figure()
ax = fig.add_subplot()

# data
ax.scatter(X, y)

# regression line
ax.plot(y_['x'], y_['y'])

# prediction interval
ax.fill_between(x_, y_['pi_lw'], y_['pi_up'],
                lw=0, color='#426e86', alpha=0.2, label='PI 95%')

# confidence interval
ax.fill_between(x_, y_['ci_lw'], y_['ci_up'],
                lw=0, color='#34675c', alpha=0.4, label='CI 95%')

ax.set_xlabel('TotalSleep')
ax.set_ylabel('LifeSpan')
ax.legend()
plt.show()
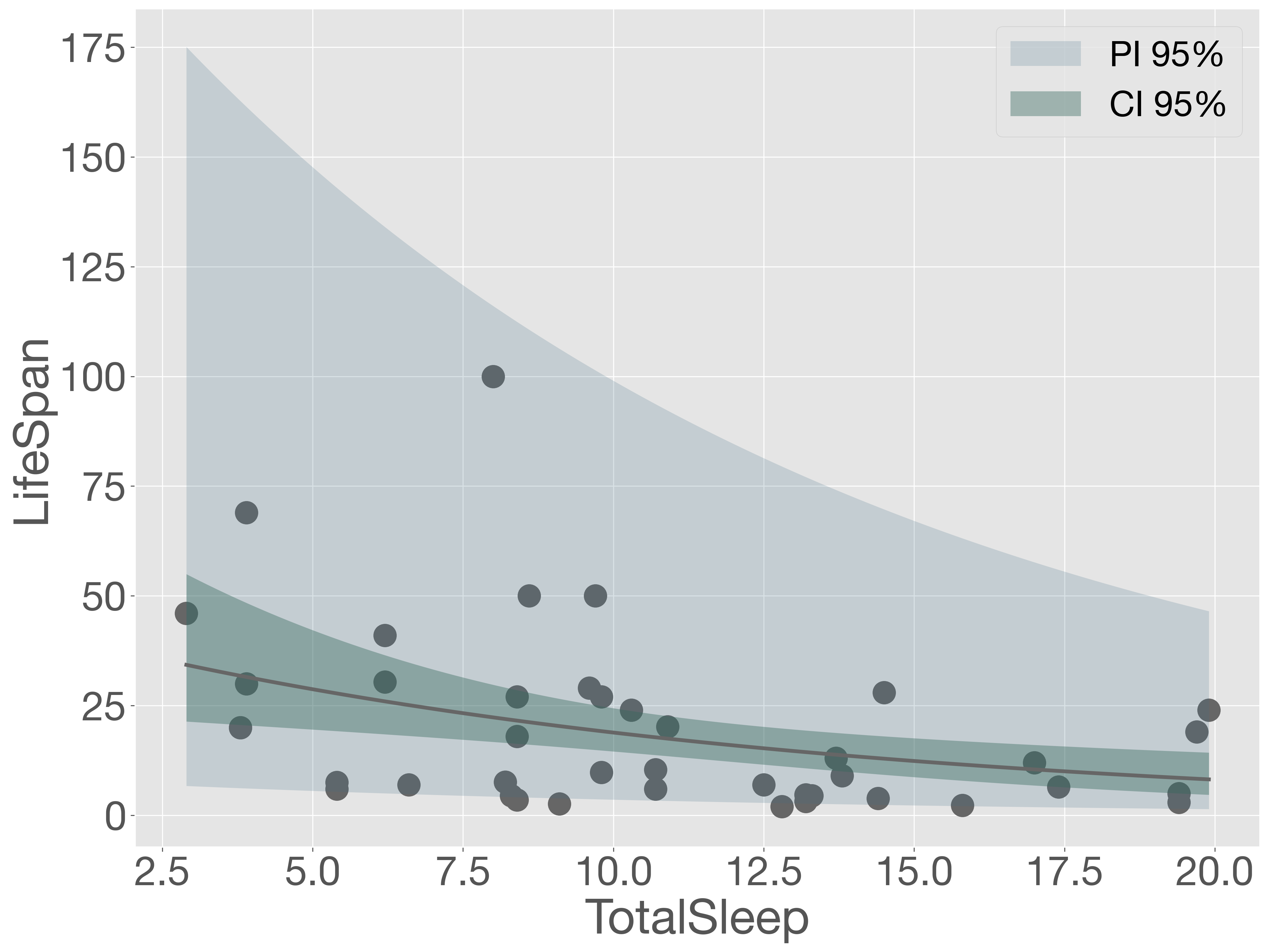
../_images/4ff074b1c8a758f00cd2b034bb2712658dc82c077602cf37d02d79a5c1885b4d.png

可視化の結果から、ほとんどの観測点が予測区間内に収まっていることが確認できました。また、AIC の値を確認しても、NegativeBinomial 関数を用いて自動的に alpha を推定したモデルは、GLM 関数を用いて alpha = 0.1 と固定したモデルよりも適合度が高いことがわかります。

fit_nb.aic

np.float64(331.4695528609516)

7.5.5. ロジスティック回帰#

ロジスティック回帰は、生物学や農学において、2 値の事象（例：生存／死亡、発芽／不発芽、感染／非感染）を説明するために広く用いられている統計手法です。ここでは、開花を制御する遺伝子の発現量が植物の開花にどのような影響を与えるかについて、ロジスティック回帰を用いて調べる例を紹介します。

まず、開花に関するデータセットを読み込みます。このデータセットには 3 列の情報が含まれており、最初の 2 列は開花を制御する遺伝子である ft と ap1 の発現量、3 列目は遺伝子発現を測定した時点でその植物が開花していたかどうか（1 は開花、0 は未開花）を示しています。

# !wget https://py.biopapyrus.jp/data/flowering.txt
flowering = pd.read_csv('flowering.txt', sep='\t')
flowering.head()
ft ap1 flowering
0 2.804565 4.439582 0
1 3.679699 8.964000 0
2 1.785063 5.256669 0
3 6.851927 7.329703 0
4 0.049923 9.580463 0

説明を簡単にするため、ここでは ft 遺伝子の発現量のみに着目して、開花の有無を説明するロジスティック回帰モデルを構築します。

X = flowering['ft']
y = flowering['flowering']

link = sm.families.links.Logit()
family = sm.families.Binomial(link)

m = sm.GLM(y, sm.add_constant(X), family=family)
fit = m.fit()

fit.summary()
Generalized Linear Model Regression Results
Dep. Variable: flowering No. Observations: 153
Model: GLM Df Residuals: 151
Model Family: Binomial Df Model: 1
Link Function: Logit Scale: 1.0000
Method: IRLS Log-Likelihood: -19.569
Date: Tue, 15 Jul 2025 Deviance: 39.137
Time: 10:40:27 Pearson chi2: 56.4
No. Iterations: 7 Pseudo R-squ. (CS): 0.4053
Covariance Type: nonrobust
coef std err z P>|z| [0.025 0.975]
const -5.4834 0.890 -6.162 0.000 -7.227 -3.739
ft 0.1826 0.035 5.196 0.000 0.114 0.252

次に、観測値とモデルの予測値をグラフに描いて、モデルを可視化します。なお、ロジスティック回帰では目的変数が 0 または 1 の値しか取らないため、通常は予測区間を描画しません。

def summarize_logit_model(x, model, link):
    x_ = sm.add_constant(x)
    
    eta = model.predict(x_, linear=True)
    cov = model.cov_params()
    se_eta = np.sqrt(np.sum(x_ @ cov * x_, axis=1))

    z = norm.ppf(0.975)

    mean_pred = link.inverse(eta)

    eta_lw = eta - z * se_eta
    eta_up = eta + z * se_eta
    ci_lw = link.inverse(eta_lw)
    ci_up = link.inverse(eta_up)

    return pd.DataFrame({
        'x': x,
        'y': mean_pred,
        'ci_lw': ci_lw,
        'ci_up': ci_up
    })




x_ = np.linspace(X.min(), X.max(), 100)
y_ = summarize_logit_model(x_, fit, link)

fig = plt.figure()
ax = fig.add_subplot()

# data
ax.scatter(X, y)

# regression line
ax.plot(y_['x'], y_['y'])

# confidence interval
ax.fill_between(x_, y_['ci_lw'], y_['ci_up'],
                lw=0, color='#34675c', alpha=0.4, label='CI 95%')

ax.set_xlabel('expression')
ax.set_ylabel('flowering')
ax.legend()
plt.show()
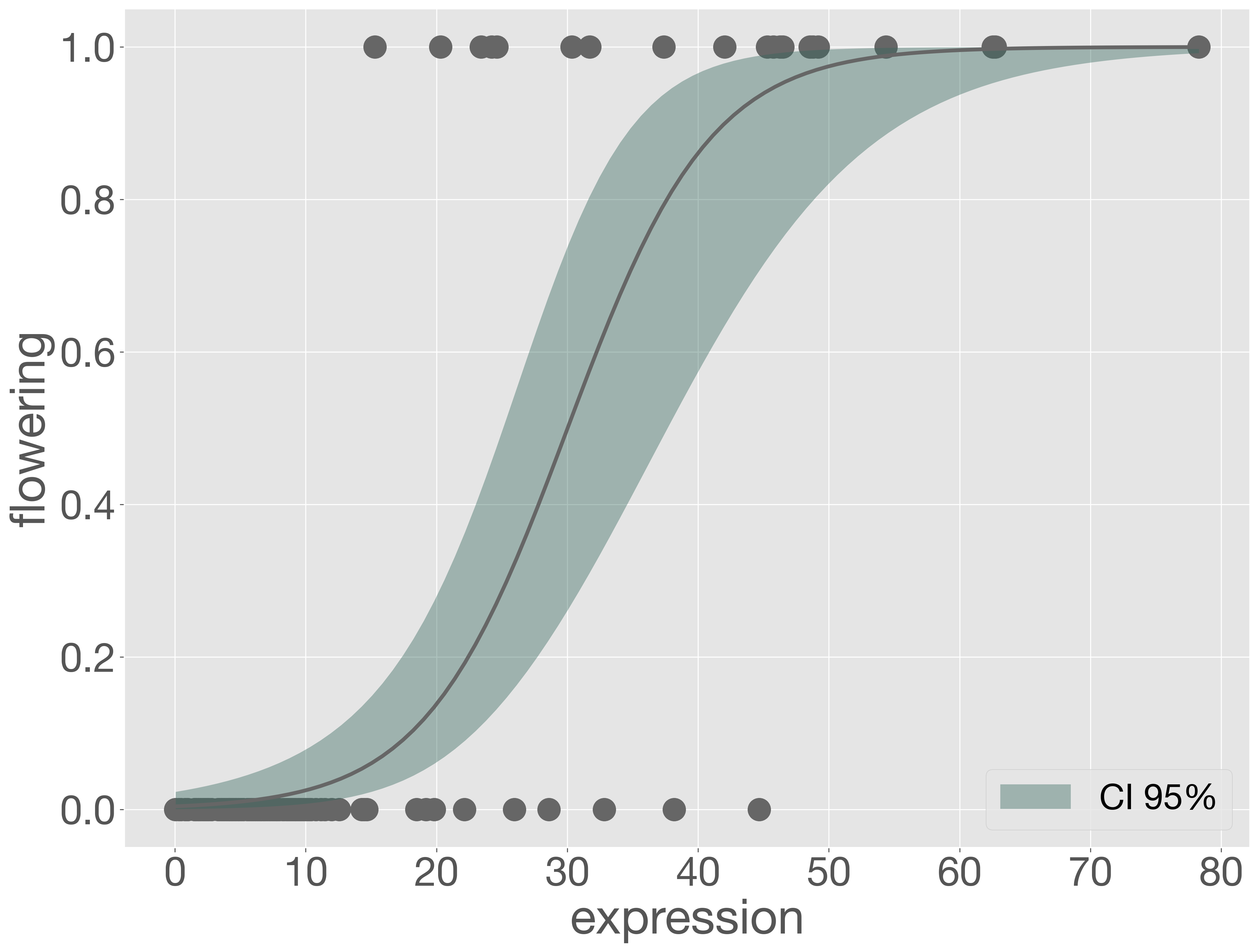
../_images/7d8e463c3c8f2e0e000cb778ee8eb34b6414b2042f33f023420f78a697435e2c.png

このように、ft 遺伝子の発現量が 30 を超えるあたりから、半数以上の個体が開花していることがわかります。さらに、発現量が 40 以上になると、約 8 割以上の個体が開花しています。この結果から、ft 遺伝子の発現量が植物の開花に強く影響を与えていることが読み取れます。

練習問題 SGL-2

植物開花データセット flowering.txt を用いて、ft 遺伝子のみ、ap1 遺伝子のみ、そして両者を同時に用いたロジスティック回帰モデルを構築しなさい。それぞれのモデルについて、AIC などの指標を用いて最適なモデルを選択してください。

結果が綺麗すぎるって？当然でしょ。これは著者が現実を削って作った、夢の世界。実務では、結果どころか、データさえ読み込めないこともあります。