6.4. 乱数#
乱数は、データ分析、機械学習、シミュレーション、統計解析など、さまざまな分野で重要な役割を果たします。NumPy の random モジュールには、さまざまな確率分布に基づいて乱数を生成する機能が用意されています。以下では、基本的な乱数の生成方法をいくつか紹介します。
平均 0、標準偏差 1 の標準正規分布に従う乱数を 10 個生成するには、次のようにします。
np.random.normal(0, 1, 10)
array([ 1.76405235, 0.40015721, 0.97873798, 2.2408932 , 1.86755799,
-0.97727788, 0.95008842, -0.15135721, -0.10321885, 0.4105985 ])
0 以上 1 未満の一様分布に従う乱数を 10 個生成するには、次のようにします。
np.random.rand(10)
array([0.79172504, 0.52889492, 0.56804456, 0.92559664, 0.07103606,
0.0871293 , 0.0202184 , 0.83261985, 0.77815675, 0.87001215])
NumPy の random モジュールは、基本的には乱数を生成するための機能を提供していますが、それをうまく活用することで、シミュレーションや統計解析など、さまざまなデータ解析に応用することができます。ここではその応用例として、モンテカルロ法による円周率の推定を紹介します。
円周率 \(\pi\) は円の直径に対する円周の長さの比率と定義されています。この定義に基けば、半径 \(r\) の円の面積は \(r \times ( \pi r) = \pi r^{2}\) となります。ここで、半径の 1 の円が XY 平面上に置かれ、円の中心が XY 平面の原点にあるとき、第一象限(\(x > 0\) かつ \(y>0\))を占め円の面積は \(\frac{\pi}{4}\) と計算されます。また、この円を外接する正方形が第一象限を占める面積は 1 となります。両者の面積比が \(\frac{\pi}{4} : 1\) となることがわかります。そこで、もしこの正方形の中にランダムに点を打ったとき、そのうち円の中に入る点の割合は、およそ \(\frac{\pi}{4}\) % となるはずです。点の数 \(n\) が十分に多ければ、円の中に入る点の数は \(n\frac{\pi}{4}\) 個となるはずです。このことを利用して円周率を推定します。
Show code cell source
n = 1000
x = np.random.rand(n)
y = np.random.rand(n)
is_inside = (x ** 2 + y ** 2 < 1)
fig = plt.figure()
ax = fig.add_subplot()
ax.scatter(x[~is_inside], y[~is_inside], c='#f39200')
ax.scatter(x[is_inside], y[is_inside], c='#31b7bc')
ax.set_aspect('equal')
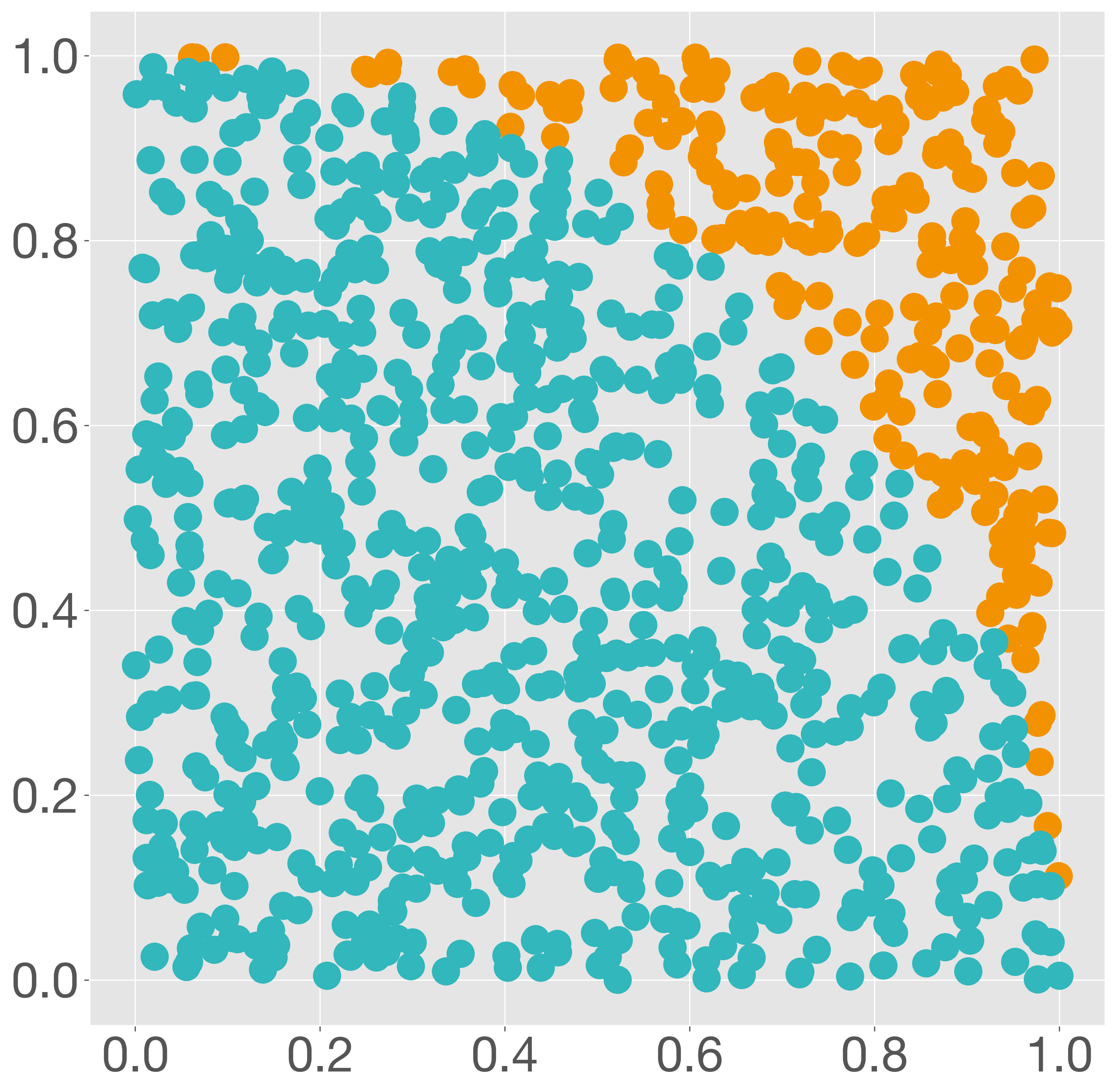
まず、\(0 \le x \le 1\) および \(0 \le y \le 1\) の範囲で点を 1 万個を打ちます。その座標を生成します。
n = 10_000
x = np.random.rand(n)
y = np.random.rand(n)
次に、円に含まれる点の数を計算します。
n_inside = np.sum(x**2 + y**2 < 1)
これをもって円周率を計算してみます。
pi = 4 * n_inside / n
pi
np.float64(3.15)
次に点の数を増やしていきましょう。推定される円周率が少しだけ正確になるのを確認できます。
n = 100_000_000
x = np.random.rand(n)
y = np.random.rand(n)
n_inside = np.sum(x**2 + y**2 < 1)
pi = 4 * n_inside / n
pi
np.float64(3.14178736)
練習問題 NR-1
「XY 平面の \(0 \le x \le 1\) および \(0 \le y \le 1\) の範囲に 1 万個の点を打ち、円周率を計算する」操作を 1000 回繰り返し、1000 回の操作で得られた 1000 個の円周率の推定値の平均を計算するプログラムを作成してください。
練習問題 NR-2
\(r\) を正の実数とします。XYZ 空間において、
を満たす点全体の立体の体積を計算するプログラムを作成してください。なお、体積計算を行う際に利用する乱数の個数を \(n\) とします。

