8.2. 分散分析#
t 検定は 2 群間の母平均に有意差があるかを検定する手法ですが、3 群以上のデータを比較する場合には使用できません。3 群以上のデータにおける母平均の差を検定するためには、分散分析(Analysis of Variance; ANOVA)を用います。分散分析は、複数の群の母平均の差異を同時に評価できるため、たとえば 3 種類以上のどんぐりの重さを比較する際に有効です。また、t 検定と同様に、分散分析においてもデータが正規分布に従うことが前提となります。データが正規分布に従っていない場合、分散分析の結果の信頼性は低下するため、検定を行う前にデータの分布を確認することが重要です。
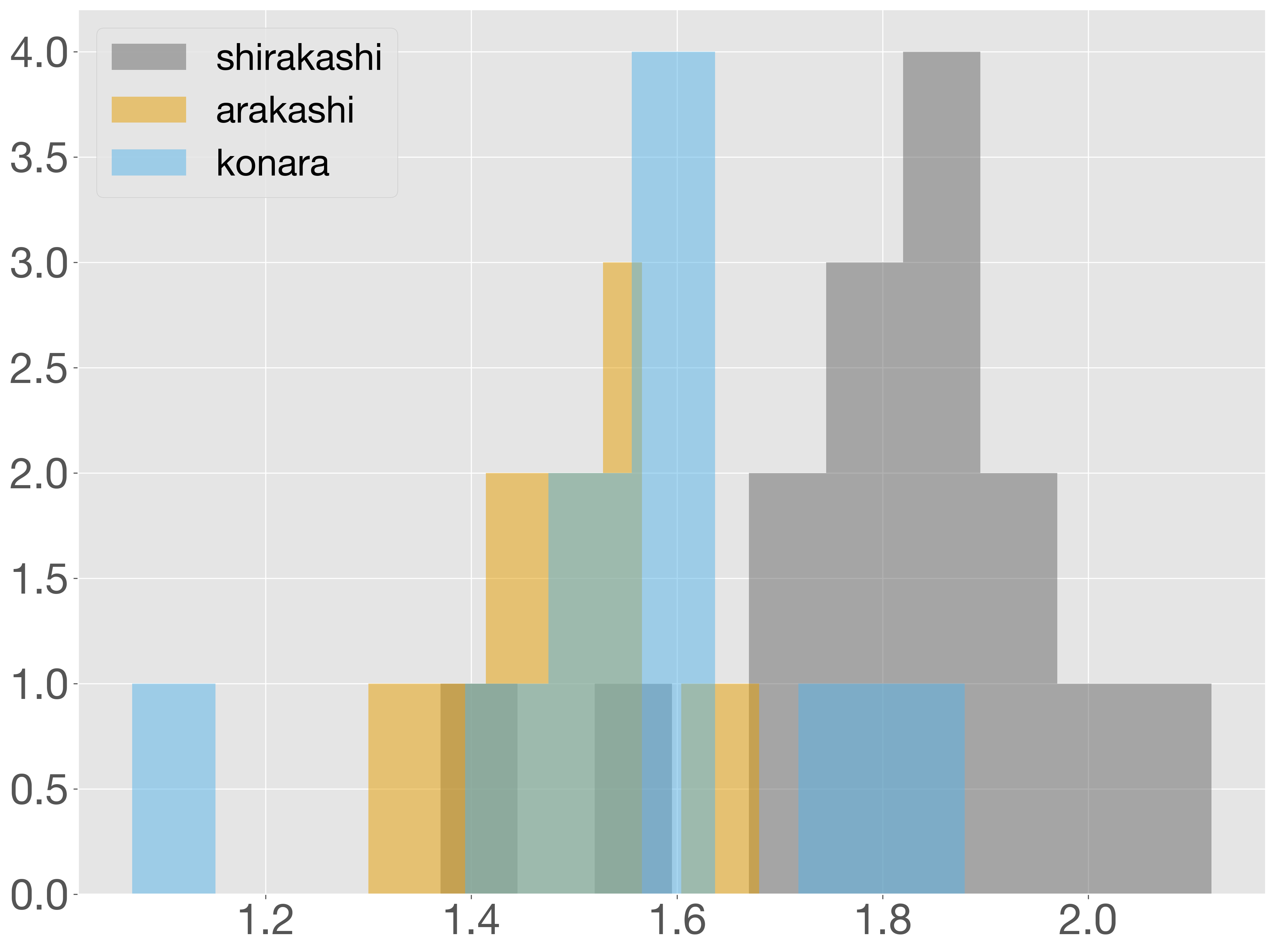
今回は、アラカシ、シラカシ、コナラの 3 種類のどんぐりの重さに違いがあるかどうかを、分散分析を用いて検定します。まず、データを準備し、各群の分布を確認します。
# !wget https://py.biopapyrus.jp/data/acorns.clean.csv
acorns_data = pd.read_csv('acorns.clean.csv')
arakashi = acorns_data['weight'][acorns_data['tree'] == 'arakashi']
shirakashi = acorns_data['weight'][acorns_data['tree'] == 'shirakashi']
konara = acorns_data['weight'][acorns_data['tree'] == 'konara']
Show code cell source
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot()
ax.hist(shirakashi, alpha=0.5, label='shirakashi')
ax.hist(arakashi, alpha=0.5, label='arakashi')
ax.hist(konara, alpha=0.5, label='konara')
ax.legend()
plt.show()
次に、「アラカシ、シラカシ、コナラのどんぐりの重さに差はない」という帰無仮説を立て、有意水準を 5% として検定を行います。分散分析は、SciPy ライブラリの stats モジュールに含まれる f_oneway 関数を使用します。
import scipy.stats as stats
res = stats.f_oneway(arakashi, shirakashi, konara)
分散分析の結果として、F 統計量と p 値が得られます。
print(res.statistic)
print(res.pvalue)
14.356705776434133
2.603440728711446e-05
F 統計量は、群間の平均の差と群内のばらつきの比率を表します。この値が大きいほど、群間に有意差がある可能性が高いといえます。また、p 値が事前に設定した有意水準よりも小さい場合、帰無仮説を棄却し、群間の平均に有意差があると統計的に結論付けることができます。今回の結果として、p 値が 0.05 より小さいため、帰無仮説を棄却し、アラカシ、シラカシ、コナラのどんぐりの平均重には有意差があると解釈できます。
なお、分散分析は群間に差があるかどうかを検定する手法であり、どの群間で差があるのかを示すものではありません。したがって、群間の平均値の差をさらに詳しく検討したい場合には、多重比較検定を行う必要があります。具体的には、Tukey 検定、Dunnett 検定、あるいは Williams 検定などを用いて、群間の差の有無を個別に検定することができます。
!rm acorns.clean.csv

