農学生命情報科学特論 I 試験問題

9.1. 農学生命情報科学特論 I 試験問題#

この試験問題に取り組む際は、以下の規則に従ってください。

  • 本ファイル（Jupyter Notebook）を直接編集し、プログラムの記述および解答を行ってください。

  • 解析用のプログラムは採点対象外です。ただし、解答が誤っている場合には、解析プログラムを参考にし、部分点を与える場合があります。

  • 解析用のプログラムは、各設問の直後に記述・実行してください。プログラムの記述は必須ではないため、省略してもかまいません。

  • 各設問への解答は、本ファイルの末尾に、英語または日本語でわかりやすく記述してください。図や表を解答中で参照する場合は、対応する解析コード内で図や表を生成し、通し番号を付け、解答文中でその番号を参照してください。なお、解答欄にはあらかじめ間違った解答例が記述されています。これを削除してください。

  • ファイルを提出する前に、Google Colab の「Run all」ボタンの右にある三角マークをクリックし、プルダウンメニューから「Clear all outputs（すべての出力をクリア）」を選択して実行してください。その後のファイルを提出してください。

  • 問題 A、B、C は必須問題で、合計 100 点満点とする。問題 D はサービス問題であり、その得点は必須問題の得点に加算される。ただし、加算後の合計点は 100 点を上限とする。

9.1.1. 問題 A (35 点)#

いきものログは、生きものに関する情報を収集・提供するシステムであり、さまざまな組織や個人が行った調査結果を集積している。集められた情報は、誰でも自由に閲覧・ダウンロードすることができる。ファイル Coreopsis_lanceolata.2025.csv.gz は、いきものログからダウンロードしたオオキンケイギクの生息調査データである。このファイルでは、各行が 1 件の報告を表し、各列にはその報告の詳細が記録されている。具体的には、生息が確認された年、月、日、緯度、経度、一次メッシュ、二次メッシュ、三次メッシュの情報が含まれる。

以下の問いに答えなさい。

# !wget https://py.biopapyrus.jp/data/Coreopsis_lanceolata.2025.csv.gz

import pandas as pd
x = pd.read_csv('Coreopsis_lanceolata.2025.csv.gz')
x.head()
year month day scientificName decimalLatitude decimalLongitude mesh1 mesh2 mesh3
0 2025 6 20.0 Coreopsis lanceolata NaN NaN 5132.0 513254.0 51325471.0
1 2025 6 20.0 Coreopsis lanceolata NaN NaN 5132.0 513254.0 51325471.0
2 2025 6 20.0 Coreopsis lanceolata NaN NaN 5132.0 513254.0 51325471.0
3 2025 6 20.0 Coreopsis lanceolata NaN NaN 5132.0 513254.0 51325471.0
4 2025 5 15.0 Coreopsis lanceolata 35.602657 139.41241 5339.0 533933.0 53393322.0

A-1 (5 点)

地図を等間隔の格子状に区切り、それぞれの格子に付けられたコードを「地域メッシュコード」と呼ぶ。日本では一次メッシュ、二次メッシュ、三次メッシュなどがよく使われている。これらのメッシュコードを用いて、生物の生息面積を推定することは可能か。

A-2（5 点）

2024 年におけるオオキンケイギクの生息に関する報告件数（行数）は何件か答えよ。

A-3（5 点）

2020 年から 2025 年までの期間において、オオキンケイギクの生息が確認された三次メッシュの数を答えよ。

A-4 (20 点)

オオキンケイギクは、一度生息が確認されると、その後は駆除できないものと仮定する。この前提に基づき、年ごとにオオキンケイギクの生息範囲がどのように変化したのかを考察せよ。

9.1.2. 問題 B (35 点)#

ファイル dragonflies.tsv.gz は、日本全国におけるトンボの生態調査結果をまとめたデータである。TSV 形式で、1 列目には調査地点の二次メッシュが記録されている。2 列目以降には、各種トンボの生息情報が記録されており、「0」はその地点で生息が確認されなかったこと、「1」は確認されたことを示している。

以下の問いに答えよ。なお、必要に応じて、緯度・経度と二次メッシュとの相互変換には、jismesh ライブラリを使用してもかまわない。

# !wget https://py.biopapyrus.jp/data/dragonflies.tsv.gz

import pandas as pd
x = pd.read_csv('dragonflies.tsv.gz', sep='\t')
x.head()
Mesh2 Sympecma_paedisca Indolestes_peregrinus Indolestes_boninensis Lestes_sponsa Lestes_dryas Lestes_temporalis Lestes_japonicus Psolodesmus_kuroiwae Mnais_costalis ... Orthetrum_poecilops Orthetrum_albistylum Orthetrum_japonicum Orthetrum_internum Orthetrum_luzonicum Orthetrum_glaucum Orthetrum_pruinosum Orthetrum_melania Libellula_quadrimaculata Libellula_angelina
0 222932 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
1 362257 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
2 362306 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 1.0 0.0 1.0 0.0 0.0 0.0
3 362327 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
4 362335 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 1.0 1.0 0.0 0.0 0.0

5 rows × 205 columns

B-1（5 点）

日本全国で生息が確認されているトンボの種数は、合計で何種か答えよ。

B-2（5 点）

弥生キャンパス（北緯 35.7165669、東経 139.7607989）から半径 20 km の範囲内で確認されたトンボの種数は、合計で何種か答えよ。

B-3（5 点）

北海道全域を「松前町（北緯 41.4919093、東経 139.4415924）より北に位置する国土（離島を含む）」と定義する。この地域で確認されたトンボの種数は何種か答えよ。

B-4（20 点）

本データに基づき、緯度または経度の違いによって確認されるトンボの種数に差が見られるかどうかを考察せよ。考察にあたっては、必要に応じて本データを可視化したグラフを用いること。また、必要に応じて先行研究や関連文献を引用してもよい。なお、文献を参照した場合は、本文中または脚注において、適切な形式で出典を明記すること。

9.1.3. 問題 C (30 点)#

ある二倍体生物からなる集団において、遺伝子型が AA、Aa、aa の個体数をそれぞれ \(n(AA)\)、\(n(Aa)\)、\(n(aa)\) とする。この集団に対して、以下の操作を行う。

  1. \(n(AA) = 600\)、\(n(Aa) = 300\)、\(n(aa) = 100\) とする。

  2. 集団からランダムに 2 個体を非復元抽出で選ぶ。

  3. 抽出したそれぞれの個体から、ランダムにアレル（A または a）を 1 つずつ取り出し、それらを組み合わせて新しい個体の遺伝子型とする。

  4. 手順 1〜2 を 1000 回繰り返し、合計で 1000 個体を生成する。

  5. \(n(AA)\)、\(n(Aa)\)、\(n(aa)\) を、手順 3 で得られた新しい個体の遺伝子型に基づいて更新する。

  6. 手順 1〜4 を 1001 回繰り返す。なお、繰り返し回数が 100 で割り切れる場合、手順 3 において生成する個体数を 10 個体とする。

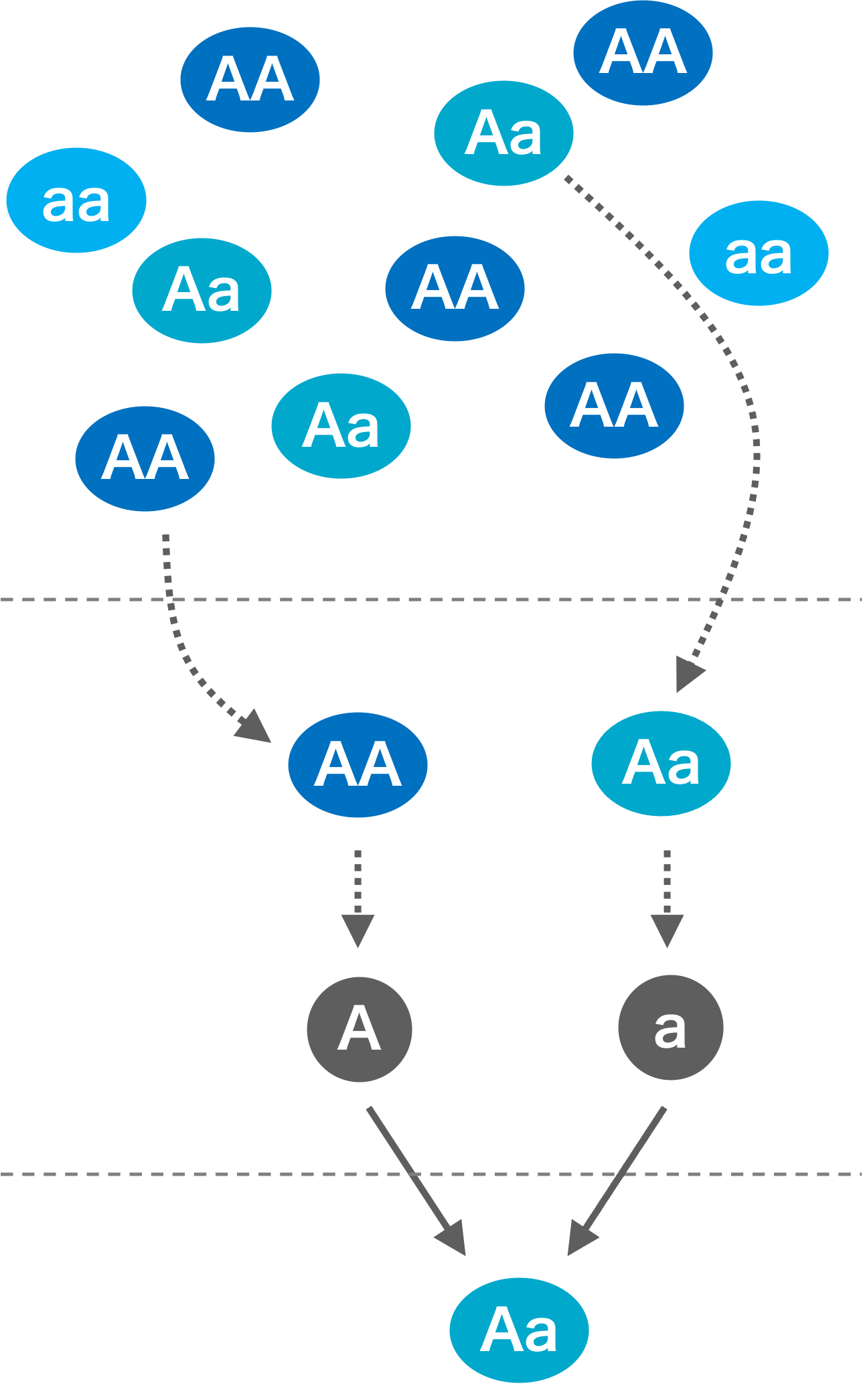
../../_images/utsp1_2025_B1.png

以下の問いに答えよ。

C-1（5 点）

手順 0〜3 を 1 回実行したとき、生成された 1000 個体のうち、遺伝子型 AA、Aa、aa の個体がそれぞれ何個体であるかを求めよ。

C-2（5 点）

手順 0〜5 まで実行したとき、各遺伝子型の個体数は最終的にどのような割合になるかを答えよ。

C-3 (20 点)

C-2 の結果が得られた理由について考察せよ。考察にあたっては、ボトルネック効果や遺伝的浮動などの専門用語を説明なしに使用して構わない。

9.1.4. 問題 D (20 点)#

あるデパートの 7 階に設置されている車椅子・ベビーカー優先エレベーターについて、日曜日午前中の利用実態を調査した。このエレベーターの定員は 16 名であるが、実際には空間的な制約により最大 8 名までしか乗れないことが分かっている。車椅子またはベビーカーは 2 名分のスペースを必要とする。さらに、ベビーカーには必ず保護者が 1 名以上付き添っている必要がある。

調査の結果、この時間帯においてエレベーターの乗員数は常に 4〜8 名の間でランダム（一様分布）であった。また、車椅子やベビーカーは、それぞれ 2 名分としてカウントされている。同時間帯には通常のエレベーターも 1 台稼働していたが、車椅子やベビーカーが乗り込むスペースはなかった。

この調査結果に基づき、以下の問いに答えよ。

D-1（10 点）

あなたがベビーカーを押して、車椅子・ベビーカー優先のエレベーターで 7 階から 1 階へ移動しようとしている。エレベーター前には他に待っている人はおらず、あなただけが待っている。このとき、あなたがエレベーターに乗れるまでに何回待つ必要があるかをシミュレーションし、その平均値と標準偏差を求めよ。

D-2（10 点） エレベーター内の利用者が 50% の確率で降りて、車椅子やベビーカーに場所を譲ると仮定する。問題 D-1 と同じ状況において、あなたが何回目でエレベーターに乗れるかをシミュレーションし、その平均値と標準偏差を求めよ。（※ 設問上は「50% が譲る」と仮定しているが、現実には車椅子やベビーカーを見ても譲らない利用者がほとんどであるというのが実情である。）

9.1.5. 解答#

9.1.5.1. A-1#

生物の生息面積を地域メッシュコードで推定することは可能。ただし、注意点としては生物がメッシュの境界を気にして動くわけではないこと。

9.1.5.2. A-2#

0 件

9.1.5.3. A-3#

4 ブロック

9.1.5.4. A-4#

オオキンケイギクが一度生息し始めたら駆除できないという前提のもとでは、年を追うごとにその生息範囲は拡大する一方であると考えられる。三次メッシュ単位で見れば、初期の数ブロックから始まり、時間とともに隣接ブロックへと侵出し、指数関数的とまではいかないまでも、じわじわと確実に勢力を広げていく様子が確認できる。地図上では派手に広がって見えるが、実際に現場に行くと「わぁ、きれい！」と写真を撮られ、駆除の話が忘れ去られるという高度な防御機構も備えている。恐るべし、キク科。

9.1.5.5. B-1#

1200 種

9.1.5.6. B-2#

1200 種

9.1.5.7. B-3#

1200 種

9.1.5.8. B-4#

東経 135 度に密集するトンボ。なぜそこなのか、問いを抱えながら三日徹夜。たどり着いた結論は、トンボは気まぐれ。

9.1.5.9. C-1#

nAA: 1 個体 nAa: 1 個体 naa: 1 個体

9.1.5.10. C-2#

nAA: 10% nAa: 10% naa: 10%

9.1.5.11. C-3#

有限個体群における遺伝子頻度の変動は、ボトルネック効果や遺伝的浮動により、理論的な期待値から外れることも珍しくない。言い換えれば、自然界は常に完璧な秩序を保つわけではなく、時には遺伝子の気まぐれが支配するランダムな揺らぎの場となる。つまり、遺伝子も「今日は気分が乗らない日」くらいのノリで動いていることがわかった。

9.1.5.12. D-1#

10.0 ± 2.5 回

9.1.5.13. D-2#

5.0 ± 2.5 回