8.1. t 検定#
t 検定(t-test)は、無作為に抽出された標本(sample)から得られたデータをもとに、全体のデータ集合である母集団(population)の平均(母平均(population mean))が特定の値と等しいかどうか、あるいは異なる母集団間で平均が等しいかどうかを調べるための統計手法です。比較するデータの性質に応じて、t 検定には以下のような種類があります。t 検定の実施には、SciPy ライブラリの stats モジュールにある関数を利用すると便利です。
1 標本 t 検定(one-sample t-test):1 つの標本に対して、その母平均が特定の値と等しいかどうかを検証します。
ttest_1samp関数を使用します。2 標本 t 検定(two-sample t-test):2 つの標本の母平均が等しいかどうかを比較します。標本間の関係性に応じて、さらに以下の 2 種類に分かれます。
対応あり 2 標本 t 検定(paired samples t-test):同じ対象に対して繰り返し測定を行った場合(たとえば同じ個体に対する処理前と処理後の比較)に用います。
ttest_rel関数を使用します。対応なし 2 標本 t 検定(independent samples t-test):異なる集団から得られた独立した標本(たとえば対照群と処理群の比較)に用います。この場合、母分散の性質によってさらに以下の 2 種類に分かれます。
ttest_ind関数を使用します。スチューデントの t 検定(Student’s t-test):母分散が等しい場合に使用します。
ttest_ind関数でequal_var=Trueを指定します。ウェルチの t 検定(Welch’s t-test):母分散が等しくない場合に使用します。
ttest_ind関数でequal_var=Falseを指定します。分散が等しい場合でもウェルチの t 検定を使用して問題ないです。そのため、実務上、分散の等質性を確認せずにウェルチの検定を用いることが一般的です。
SciPy ライブラリの stats モジュールは、通常 scipy.stats を stats として省略してインポートします。
import scipy.stats as stats
分析対象のデータを準備します。ここでは、どんぐりのデータセットからアラカシ(arakashi)とシラカシ(shirakashi)のデータを抽出し、両者の重さ(weight)に有意な差があるかどうかを検定します。まずは該当するデータを取り出します。
# !wget https://py.biopapyrus.jp/data/acorns.clean.csv
acorns_data = pd.read_csv('acorns.clean.csv')
arakashi = acorns_data['weight'][acorns_data['tree'] == 'arakashi']
shirakashi = acorns_data['weight'][acorns_data['tree'] == 'shirakashi']
次に、アラカシとシラカシのどんぐりの重さの分布をヒストグラムで可視化します。t 検定は、データが正規分布に従うことを前提としているため、検定を行う前に分布を視覚的に確認する習慣をつけておくとよいでしょう。
Show code cell source
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot()
ax.hist(shirakashi, alpha=0.5, label='shirakashi')
ax.hist(arakashi, alpha=0.5, label='arakashi')
ax.legend()
plt.show()
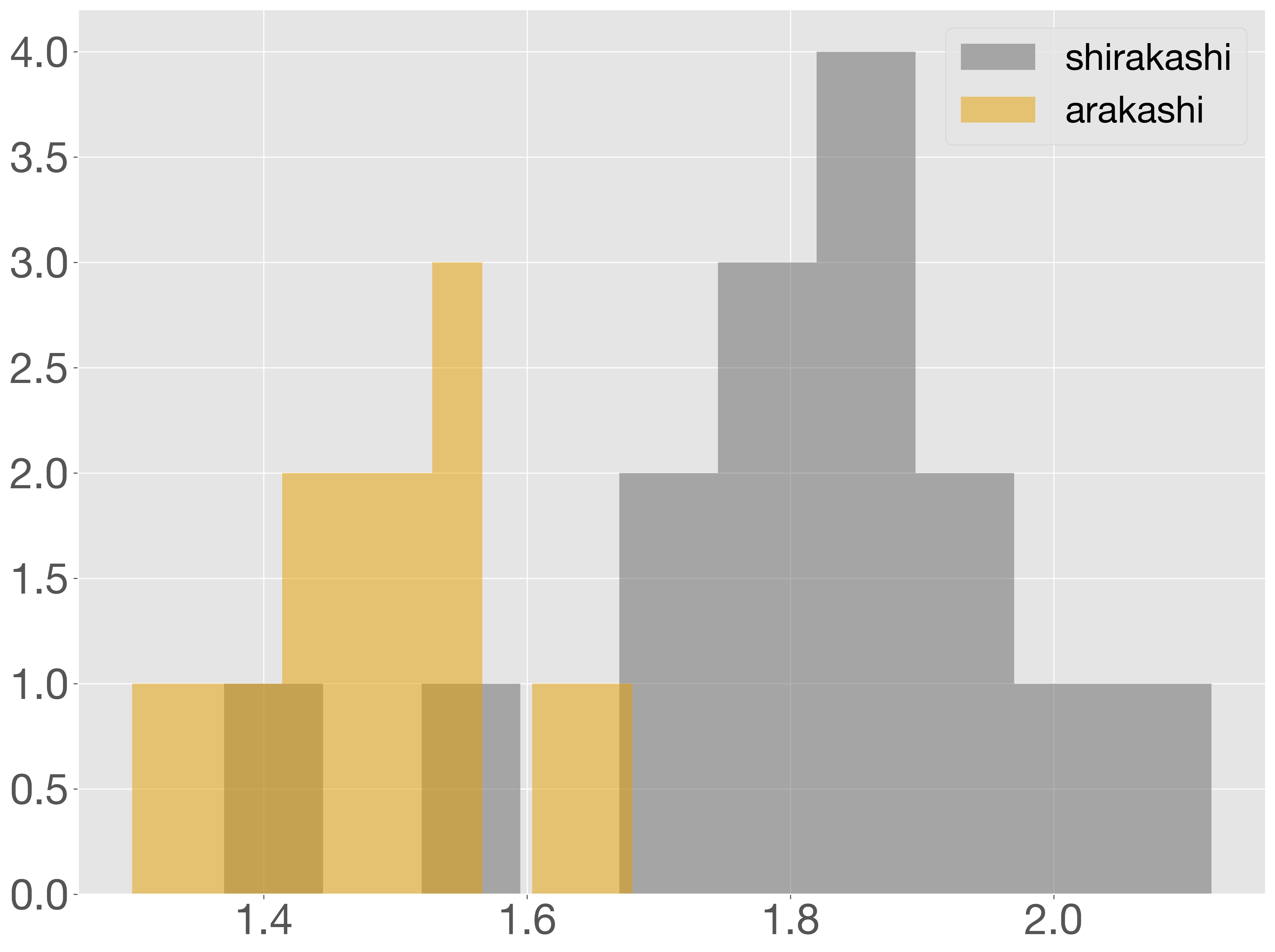
ヒストグラムから、両者の分布が正規分布の形状と大きくかけ離れていないことが確認できます。以降では、両者が正規分布に従うものとして分析を進めます。
なお、データが正規分布に従っているかどうかを統計的に評価するためには、Shapiro-Wilk 検定などの正規性検定を用いる必要があります。しかし、正規性検定の後に t 検定を行うと、多重検定によって偽陽性(第 I 種の誤り)のリスクが高まる可能性があります。そのため、実務では、まずヒストグラムでデータの分布を確認し、形状がおおよそ正規分布に近いと判断できる場合には、正規性検定を省略しても問題ないことが多いです。
8.1.1. 1 標本 t 検定#
1 標本 t 検定は、1 つの母集団から無作為に抽出された標本に基づき、母集団の平均が特定の値と等しいかどうかを検証するための方法です。たとえば、「アラカシのどんぐりの重さが 1.55g に等しいかどうか」を統計的に判断する場面で利用されます。
検定を行うにあたっては、まず「アラカシの母集団におけるどんぐりの重さは 1.55g である」という仮説を立てます。この仮説は帰無仮説(null hypothesis)と呼ばれます。次に、結果の信頼性を評価するために、有意水準(significance level)を設定します。有意水準とは、帰無仮説が正しいにもかかわらず、誤って棄却してしまう確率のことで、危険率とも呼ばれます。生物学や農学の分野では、一般的に 5%(0.05)または 1%(0.01)が用いられます。
その後、帰無仮説のもとで、標本から得られた平均と仮定された値(1.55)との差を統計的に評価します。実際には、母平均の 95% または 99% 信頼区間を推定し、その区間に仮定した値(1.55)が含まれているかどうかを確認します。検定の結果として、p 値(p-value)が算出されます。p 値とは、「帰無仮説が正しいとしたときに、現在得られたデータが観測される確率」を意味します。p 値が設定した有意水準(たとえば 0.05)よりも小さければ帰無仮説を棄却(rejection)することができます。
このような計算は本来数式を用いて行いますが、SciPy の stats モジュールにある ttest_1samp 関数を使えば、簡単に実行できます。
res = stats.ttest_1samp(arakashi, 1.55)
res.confidence_interval(0.95)
ConfidenceInterval(low=np.float64(1.4289676419926463), high=np.float64(1.5467466437216397))
推定された母平均の 95% 信頼区間を確認すると、この区間に 1.55 が含まれていません。したがって、帰無仮説である「アラカシの母集団のどんぐりの重さは 1.55g である」は成立しないと考えるのが妥当です。言い換えれば、アラカシのどんぐりの重さは 1.55g とは統計的に言えない、という結論になります。
次に、p 値を確認して帰無仮説を採択するか棄却するかを判断します。
res.pvalue
np.float64(0.04013989587452353)
p 値が、事前に設定した有意水準(5%)よりも小さいため、帰無仮説「アラカシの母集団のどんぐりの重さは 1.55g である」は棄却できます。つまり、有意水準 5% のもとでは、アラカシの母集団のどんぐりの重さが 1.55g であるとは言えない、ということになります。
ただし、この結論は設定した有意水準に基づいており、有意水準を変えると結論が変わる可能性があります。たとえば、99% 信頼区間(有意水準 1%)を用いた場合、帰無仮説を棄却できなくなることもあります。p 値を確認してから有意水準を決めるのではなく、検定の前に有意水準をあらかじめ設定しなければなりません。
res = stats.ttest_1samp(arakashi, 1.55)
res.confidence_interval(0.99)
ConfidenceInterval(low=np.float64(1.4057454995143839), high=np.float64(1.569968786199902))
8.1.2. 対応あり 2 標本 t 検定#
対応のある 2 標本 t 検定は、同じ母集団から抽出した標本を異なる条件や時点で測定し、それらの平均に差があるかどうかを検定する方法です。この検定は、2 つの標本が対応している(ペアになっている)場合に使用されます。たとえば、どんぐりを採取してすぐに測定した重さと、2 週間乾燥させた後の重さを比較して、重さに変化があったかどうかを検証する場合などに用いられます。
ここでは、乾燥処理前後のどんぐりの重さに有意な変化があったかどうかを検定します。検定にあたっては、帰無仮説として「処理前と処理後の母平均の差は 0 である」と設定します。また、有意水準は 5% に設定します。実際の計算では、処理前後の標本平均の差に対して 95% 信頼区間を推定し、その区間に 0 が含まれているかどうかを確認します。これらの計算は、ttest_rel 関数を使って実行できます。
w_wet = [2.80, 2.54, 2.28, 2.33, 2.41]
w_dry = [2.20, 2.08, 2.02, 2.15, 2.00]
res = stats.ttest_rel(w_wet, w_dry)
res.confidence_interval(0.95)
ConfidenceInterval(low=np.float64(0.17601845856567355), high=np.float64(0.5879815414343263))
res.pvalue
np.float64(0.006749051333402455)
処理前後の標本平均の差の 95% 信頼区間には 0 が含まれていません。また、p 値も事前に設定した有意水準(5%)を下回っています。つまり、有意水準 5% のもとで、乾燥前と乾燥後でどんぐりの重さに有意な差が見られたと判断するのが妥当です。
8.1.3. 対応なし 2 標本 t 検定#
対応なしの 2 標本 t 検定は、比較する 2 群に共通の(対応した)個体が存在しない場合に使用されます。たとえば、アラカシとシラカシのどんぐりの重さが同じかどうかを比較する場合に使用されます。
ここでは、アラカシとシラカシのどんぐりの重さに違いがあるかどうかを検定してみましょう。検定を行うにあたり、「アラカシとシラカシのどんぐりの重さは同じである」という帰無仮説を立て、有意水準を 5% に設定します。実際の検定では、それぞれの標本の平均を計算し、両者の差の 95% 信頼区間に 0 が含まれているかどうかを確認します。ttest_ind 関数を使ってこの検定を行います。
なお、比較する 2 つの母集団が独立している場合、厳密にはそれぞれの母分散が同じかどうかを確認する必要があります。もし分散が同じであれば、ttest_ind 関数を実行する際に equal_var=True として検定を行います。この検定をスチューデントの t 検定と呼びます。一方、分散が異なる場合は equal_var=False として検定を行います。これをウェルチの t 検定と言います。両者の分散が同じかどうかを確認するために別の検定(たとえば F 検定など)を行うこともできますが、検定を重ねることで偽陽性が増えるリスクがあります。そのため、通常は分散が異なる前提でウェルチの t 検定を行うことが一般的です。
res = stats.ttest_ind(arakashi, shirakashi, equal_var=False)
res.confidence_interval(0.95)
ConfidenceInterval(low=np.float64(-0.4310098922587564), high=np.float64(-0.20527582202695815))
res.pvalue
np.float64(6.7526869096482e-06)
比較する 2 つの実験群の母平均の差の 95% 信頼区間に 0 が含まれていないことが確認できます。また、検定結果の p 値が事前に設定した有意水準(5%)よりも小さいことも確認できます。つまり、有意水準 5% のもとで帰無仮説を棄却でき、アラカシとシラカシのどんぐりの重さに有意な差があると解釈するのが妥当です。
検定を行う際に方向を指定しない場合、ttest_ind 関数では両側検定(two-sided test)が実行されます。つまり、検定対象となる 2 つの標本の母平均の大小関係がわからない状況下で、両者の母平均に有意差があるかどうかを検定しています。これに対して、片側検定(one-sided test)は、母平均の大小関係が予測できる場合に使用されます。片側検定は分布の片側のみを考慮するため、有意差が出やすい傾向があります。
統計的検定の正しい手順では、帰無仮説を立てた後に実験を行い、データを収集してから検定を実施します。このため、実験前に一方が他方より大きいという確実な情報を持っていないことが一般的であり、両側検定を行うのが一般的です。実験後に得られたデータの平均を見てから片側検定を行うのは、統計的には不適切です。つまり、「結果を見てから検定の方向を決める」のは、成績表を見てから志望校を下げるのと同じくらいズルいのです。
ttest_ind 関数で片側検定を行うには、引数 alternative に 'greater' または 'less' を指定します。最初のサンプルが 2 番目のサンプルより大きいと予想される場合は 'greater' を、逆の場合は 'less' を指定します。たとえば、データ収集前に「シラカシのどんぐりがアラカシのどんぐりよりも重い」という確実な情報がある場合は、次のように片側検定を行うことができます。
res = stats.ttest_ind(arakashi, shirakashi, equal_var=False, alternative='less')
res.pvalue
np.float64(3.3763434548241e-06)

