8.4. 線形回帰#
回帰(regression)とは、ある変数(結果)が別の変数(原因)に影響されて変化する関係を探る手法です。この関係を数式で表現し、原因と結果の結びつきを定量的に分析したり、将来を予測したりする方法を回帰分析(regression analysis)と呼びます。たとえば、天候や土壌条件が作物の収量に与える影響を分析したり、気象条件から植物病害虫の発生リスクや農作物の市場価格を予測したりする際に活用されます。
回帰には、線形回帰(linear regression)と非線形回帰がありますが、生物学や農学の分野では多くの場合、線形回帰が用いられます。回帰分析において、原因となる変数を説明変数(explanatory variable)、結果となる変数を目的変数(objective variable)と呼びます。説明変数を \(X\)、目的変数を \(Y\) としたとき、線形回帰は次のような式で表されます。
ここで、\(\beta_{0}\) は切片、\(\beta_{1}\) は説明変数に対する回帰係数、\(\epsilon\) は誤差項です。
また、目的変数に影響を与える要因が複数あると考えられる場合は、\(n\) 個の説明変数を用いて次のように表現します。
このとき、\(\beta_{1}, \beta_{2}, \cdots, \beta_{n}\) はそれぞれの説明変数に対応する回帰係数です。実験や調査で得られた \(X\) および \(Y\) のデータをもとに、これらの係数を推定します。推定された回帰係数を用いて得られる式(例:\(y = 1.2 + 1.6x_{1} + 0.8x_{2} + \cdots + 0.2x_{n}\))を、回帰直線、回帰モデル、あるいは単にモデルと呼びます。
線形回帰のうち、説明変数が 1 つだけの場合を線形単回帰(simple linear regression)、複数ある場合を線形重回帰(multiple linear regression)と呼びます。ただし、実用上、単回帰が使用される場面は少なく、実際には複数の説明変数を用いる重回帰が一般的です。そのため、一般に「回帰」や「回帰分析」と言えば、重回帰と考えて差し支えありません。
また、回帰モデルでは誤差項が正規分布に従うことが前提とされます。したがって、モデル構築後には、モデルによる予測値と実測値の誤差を可視化し、その誤差の分布が適切かどうかを確認する必要があります。
Python を用いて回帰分析を行う際には、主に statsmodels と scikit-learn の 2 つのライブラリが利用されます。statsmodels は統計的解析に適しており、回帰係数の推定、パラメータに対する検定、予測区間や信頼区間の算出などが可能です。一方、scikit-learn は回帰分析を機械学習の一手法として扱い、予測に重点を置いたモデリングに適しています。本節では、推定されたモデルを評価したり、信頼区間の確認したりするなどの統計的な観点を重視するため、statsmodels を使用して解説を進めます。
8.4.1. 単回帰#
どんぐりの高さ(height)を使ってその重さ(weight)を予測する回帰モデルを作成してみましょう。まず、Pandas を使ってどんぐりのデータを読み込みます。どんぐりは種類によって形が異なり、例えばクヌギは丸く、マテバシイは細長い形状をしています。そのため、すべての種類のデータをまとめて扱うと、形状の違いによってモデルの精度が下がる可能性があります。そこで今回は、クヌギのどんぐりのデータだけを抽出し、分析対象とします。モデルの作成には重さと高さの情報だけが必要なので、これら 2 列だけを取り出します。
# !wget https://py.biopapyrus.jp/data/acorns.clean.csv
acorns_data = pd.read_csv('acorns.clean.csv')
kunugi = acorns_data.loc[acorns_data['tree'] == 'kunugi', ['weight', 'height']]
kunugi
| weight | height | |
|---|---|---|
| 0 | 5.55 | 2.27 |
| 1 | 4.62 | 1.98 |
| 2 | 5.05 | 2.08 |
| 3 | 5.44 | 2.18 |
| 4 | 5.60 | 2.20 |
| 5 | 4.83 | 2.19 |
| 6 | 5.55 | 2.16 |
| 7 | 5.13 | 2.20 |
| 8 | 6.03 | 2.26 |
| 9 | 7.41 | 2.35 |
次に、statsmodels ライブラリの api モジュールが提供する OLS 関数を使って回帰係数を推定してみましょう。OLS 関数では、目的変数と説明変数をそれぞれ引数として与えます。このとき、回帰モデルに定数項(\(\beta_0\))を含めるために、add_constant 関数を使って説明変数に定数列(すべての値が 1)を追加する必要があります。以下は、クヌギのどんぐりデータを用いて回帰モデルを構築する例です。
import statsmodels.api as sm
from statsmodels.formula.api import ols
X = kunugi['height']
y = kunugi['weight']
model = sm.OLS(y, sm.add_constant(X))
results = model.fit()
推定された回帰モデルの結果は、results オブジェクトに保存されます。モデルの詳細な概要を確認するには、次のように summary() メソッドを使用します。
results.summary()
| Dep. Variable: | weight | R-squared: | 0.644 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.600 |
| Method: | Least Squares | F-statistic: | 14.48 |
| Date: | Thu, 09 Oct 2025 | Prob (F-statistic): | 0.00520 |
| Time: | 13:17:53 | Log-Likelihood: | -6.0395 |
| No. Observations: | 10 | AIC: | 16.08 |
| Df Residuals: | 8 | BIC: | 16.68 |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | -7.8974 | 3.530 | -2.237 | 0.056 | -16.037 | 0.242 |
| height | 6.1355 | 1.612 | 3.805 | 0.005 | 2.417 | 9.854 |
| Omnibus: | 0.326 | Durbin-Watson: | 1.805 |
|---|---|---|---|
| Prob(Omnibus): | 0.850 | Jarque-Bera (JB): | 0.148 |
| Skew: | 0.224 | Prob(JB): | 0.929 |
| Kurtosis: | 2.608 | Cond. No. | 59.7 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
また、推定された回帰係数を確認したい場合は、次のようにします。
results.params
const -7.897444
height 6.135548
dtype: float64
今回構築した回帰モデルでは、説明変数はどんぐりの「高さ」のみです。このため、回帰式は weight = 6.14height - 7.9 のような一次式となります。
この回帰式をもとに、観測データと回帰直線を重ねてグラフで可視化してみましょう。回帰直線を描くためには、説明変数(どんぐりの高さ)と、それに対応する予測値のペアが少なくとも 2 組必要です。ここでは、回帰モデルを構築する際に使用したデータを基に、どんぐりの高さの最小値と最大値をモデルに入力し、それぞれの予測値を算出します。続けて、これら 2 点を結ぶことで回帰直線を描画します。
以下のコードでは、モデルの predict メソッドを用いて予測値を算出し、plot メソッドを使って回帰直線を描いています。さらに、測定値は scatter メソッドを用いて、同じグラフ上に散布図として重ねて表示します。
fig = plt.figure()
ax = fig.add_subplot()
# observed data
ax.scatter(X, y)
# regression line
x_ = [X.min(), X.max()]
y_ = results.predict(sm.add_constant(x_))
ax.plot(x_, y_)
ax.set_xlabel('height')
ax.set_ylabel('weight')
plt.show()
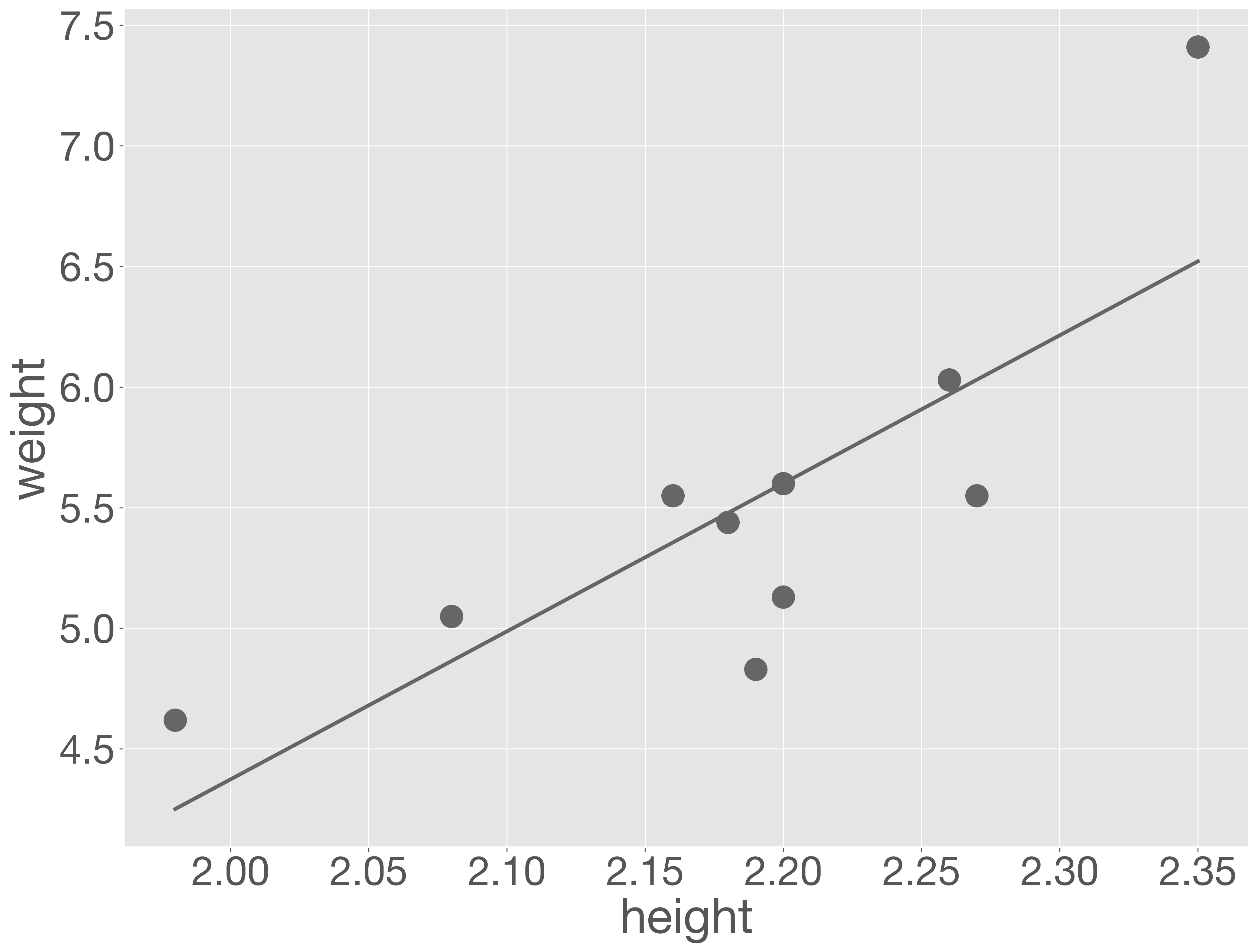
モデルの妥当性を検討するためには、予測値と観測値の差である残差のパターンを確認することが重要です。残差が説明変数の値に依存せず、正規分布している場合、モデルは妥当である可能性が高くなります。以下のコードは、各サンプルの誤差を視覚的に示しています。
err = y - results.predict(sm.add_constant(X))
fig = plt.figure()
ax1 = fig.add_subplot(1, 2, 1)
ax1.plot([X.min(), X.max()], [0, 0])
ax1.vlines(X, 0, err, linestyles='dashed')
ax1.scatter(X, err)
ax1.set_xlabel('height')
ax1.set_ylabel('error')
ax2 = fig.add_subplot(1, 2, 2)
ax2.hist(err)
plt.show()
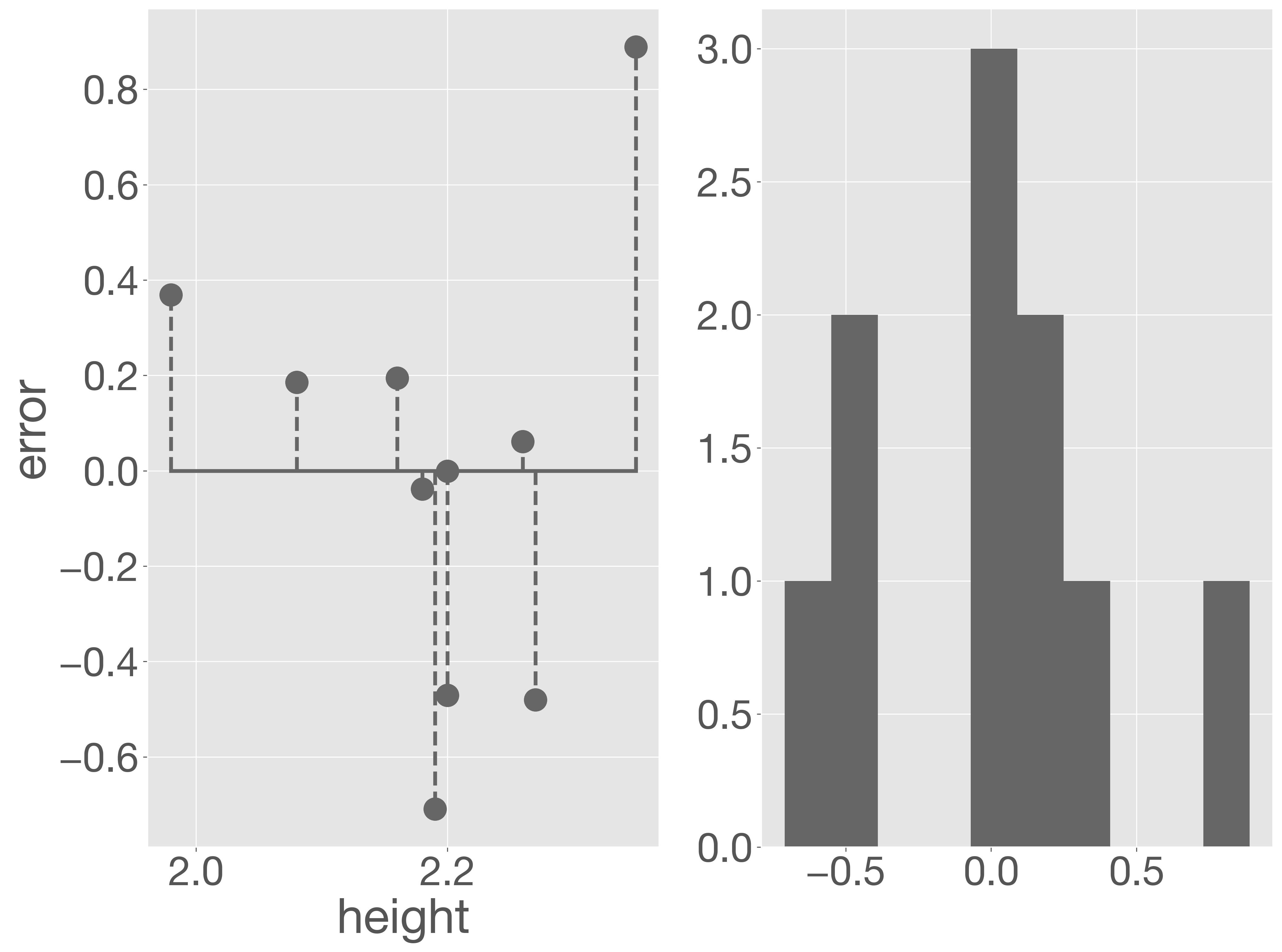
予測誤差の大きいどんぐりが含まれるものの、予測誤差の分布は正規分布に近いため、モデルとしては妥当と考えられれます。
回帰モデルは、分析に用いたどんぐりのデータセットに基づいて推定されたものです。そのため、同じ条件でデータを再び収集したとしても、得られる回帰直線は毎回少しずつ異なる可能性があります。仮に、同様の実験を無数に繰り返したとすると、無数の異なる回帰直線が描かれることになります。ここで、もしどんぐりの重さと高さの間に真の比例関係が存在するならば、これらの回帰直線の傾きや切片は、ある特定の値に近づいて収束し、回帰直線もある範囲内に収まると考えられます。このような無数の回帰直線のうち、95% が通ると予想される範囲を 95% 信頼区間(confidence interval; CI)と呼びます。
信頼区間に似た概念として、予測区間(prediction interval; PI)があります。信頼区間が再実験によって得られる回帰直線が通る範囲を示すのに対し、予測区間は再実験で得られる新たなデータ点が存在する範囲を示します。
信頼区間および予測区間を計算するには、モデルの get_prediction メソッドに説明変数の値を代入します。これにより、それぞれの説明変数に対応する信頼区間および予測区間が計算されます。計算結果は、summary_frame メソッドを用いることで、データフレームとして取得できます。
なお、信頼区間や予測区間の幅は一定ではなく、説明変数の値に応じて変化します。そのため、信頼区間や予測区間をより正確に把握するには、説明変数の値を複数用意する必要があります。ここでは、モデル構築に使用したデータの最小値から最大値までを 100 等分し、その値を説明変数としてモデルに代入して予測を行います。
x_ = np.linspace(X.min(), X.max(), 100)
y_ = results.get_prediction(sm.add_constant(x_))
y_sum = y_.summary_frame(alpha=0.05)
y_sum.head()
| mean | mean_se | mean_ci_lower | mean_ci_upper | obs_ci_lower | obs_ci_upper | |
|---|---|---|---|---|---|---|
| 0 | 4.250942 | 0.368629 | 3.400881 | 5.101002 | 2.827916 | 5.673967 |
| 1 | 4.273872 | 0.363182 | 3.436373 | 5.111372 | 2.858314 | 5.689431 |
| 2 | 4.296803 | 0.357754 | 3.471821 | 5.121785 | 2.888615 | 5.704992 |
| 3 | 4.319734 | 0.352345 | 3.507225 | 5.132243 | 2.918817 | 5.720651 |
| 4 | 4.342665 | 0.346956 | 3.542582 | 5.142747 | 2.948918 | 5.736412 |
次に、信頼区間と予測区間をグラフに描画してみます。
fig = plt.figure()
ax = fig.add_subplot()
# data
ax.scatter(X, y)
# regression line
ax.plot(x_, y_sum['mean'])
# prediction interval
ax.fill_between(x_, y_sum['obs_ci_lower'], y_sum['obs_ci_upper'],
lw=0, color='#426e86', alpha=0.2, label='PI 95%')
# confidence interval
ax.fill_between(x_, y_sum['mean_ci_lower'], y_sum['mean_ci_upper'],
lw=0, color='#34675c', alpha=0.4, label='CI 95%')
ax.set_xlabel('height')
ax.set_ylabel('weight')
ax.legend()
plt.show()
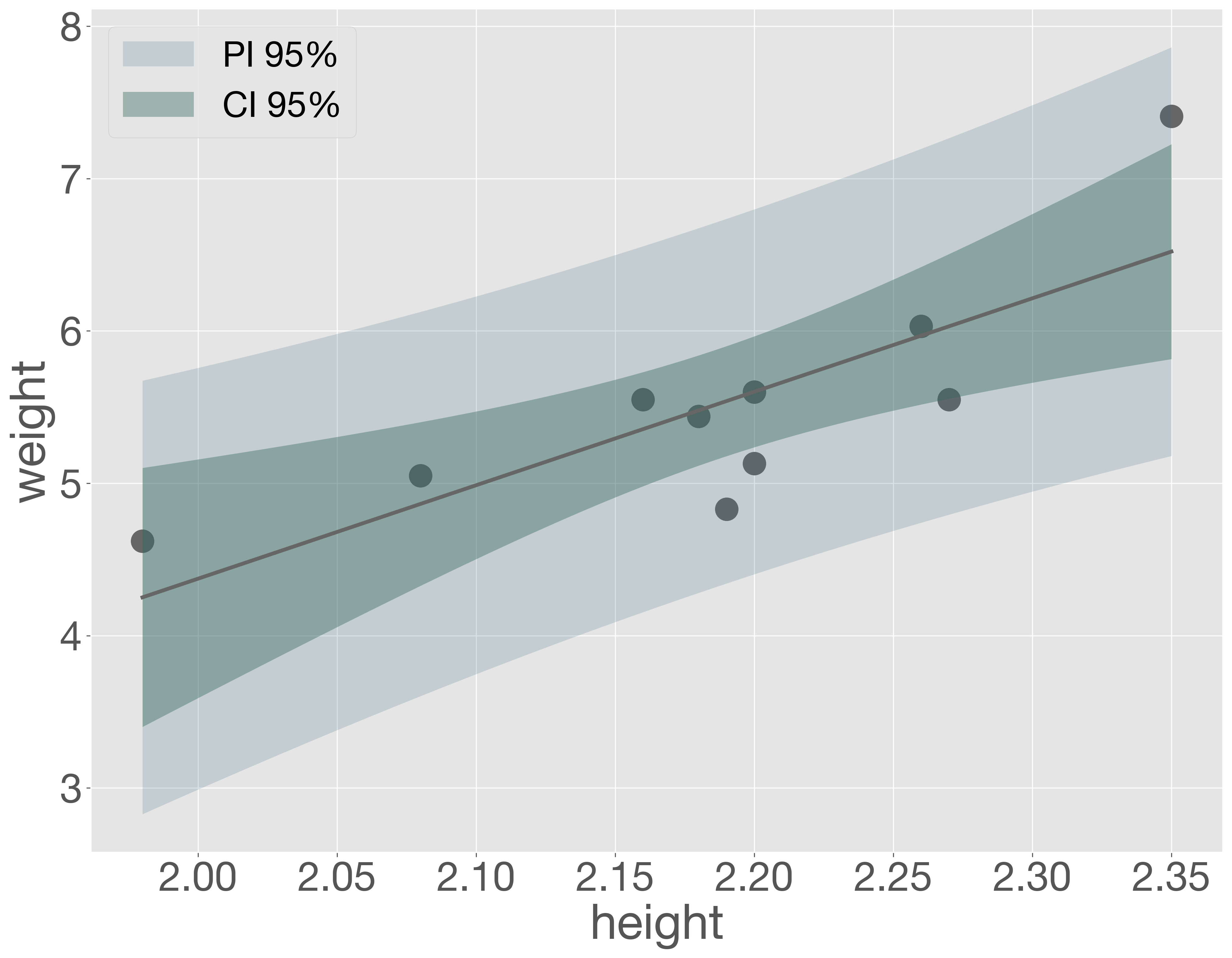
練習問題 SLM-2
どんぐりデータセット(acorns.clean.txt)を読み込み、各種どんぐりに対して、高さ(height)で重さ(weight)を説明する単回帰モデルを構築し、どんぐりの形と推定される回帰直線の傾きの間にどのような関係があると思われるのかを簡潔に答えよ。
8.4.2. 重回帰#
説明変数が複数ある場合の回帰分析を見ていきましょう。クヌギのどんぐりの重さ(weight)を推定するために、どんぐりの高さ(height)と直径(diameter)の 2 つの説明変数を使います。まず、解析対象のデータを抽出します。
acorns_data = pd.read_csv('acorns.clean.csv')
X = acorns_data.loc[acorns_data['tree'] == 'kunugi', ['height', 'diameter']]
y = acorns_data['weight'][acorns_data['tree'] == 'kunugi']
説明変数が複数ある場合、各変数の単位や値の範囲が異なることが多いため、そのままで回帰係数を推定すると、どの説明変数が目的変数に強く影響を与えているのかを適切に分析することができません。そこで、回帰を行う前に、すべての説明変数が平均 0、分散 1 となるように標準化(standardization)を行います。標準化を行うことで、各説明変数が同じスケールで評価され、モデルの解釈がしやすくなります。この場合、weight 列以外のすべての列に対して正規化を行います。
X = (X - X.mean()) / X.std()
X.describe()
| height | diameter | |
|---|---|---|
| count | 1.000000e+01 | 1.000000e+01 |
| mean | 2.153833e-15 | 4.884981e-16 |
| std | 1.000000e+00 | 1.000000e+00 |
| min | -2.023220e+00 | -1.055621e+00 |
| 25% | -2.150282e-01 | -6.540261e-01 |
| 50% | 7.819208e-02 | -3.098018e-01 |
| 75% | 5.668925e-01 | 5.794442e-01 |
| max | 1.593164e+00 | 2.157139e+00 |
続けて、OLS 関数に目的変数、定数列を追加した説明変数を順に与えて、モデルを構築します。
model = sm.OLS(y, sm.add_constant(X))
results = model.fit()
results.summary()
| Dep. Variable: | weight | R-squared: | 0.943 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.927 |
| Method: | Least Squares | F-statistic: | 58.28 |
| Date: | Thu, 09 Oct 2025 | Prob (F-statistic): | 4.33e-05 |
| Time: | 13:17:56 | Log-Likelihood: | 3.1487 |
| No. Observations: | 10 | AIC: | -0.2974 |
| Df Residuals: | 7 | BIC: | 0.6104 |
| Df Model: | 2 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 5.5210 | 0.067 | 82.708 | 0.000 | 5.363 | 5.679 |
| height | 0.2569 | 0.093 | 2.759 | 0.028 | 0.037 | 0.477 |
| diameter | 0.5662 | 0.093 | 6.080 | 0.001 | 0.346 | 0.786 |
| Omnibus: | 0.535 | Durbin-Watson: | 1.513 |
|---|---|---|---|
| Prob(Omnibus): | 0.765 | Jarque-Bera (JB): | 0.463 |
| Skew: | -0.411 | Prob(JB): | 0.794 |
| Kurtosis: | 2.340 | Cond. No. | 2.19 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
results.params
const 5.521000
height 0.256928
diameter 0.566173
dtype: float64
回帰式は weight = 5.521 + 0.257height + 0.566diameter のように推定されました。係数の大きさから、クヌギのどんぐりの重さを説明するには、高さよりも直径の方がより有効であると考えられます。
次に、細長い形状を持つコナラのどんぐりに対して、同様の回帰モデルを構築して分析してみよう。
Show code cell content
X_konara = acorns_data.loc[acorns_data['tree'] == 'konara', ['height', 'diameter']]
X_konara = (X_konara - X_konara.mean()) / X_konara.std()
y_konara = acorns_data['weight'][acorns_data['tree'] == 'konara']
model_konara = sm.OLS(y_konara, sm.add_constant(X_konara))
results_konara = model_konara.fit()
results_konara.summary()
| Dep. Variable: | weight | R-squared: | 0.784 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.722 |
| Method: | Least Squares | F-statistic: | 12.67 |
| Date: | Thu, 09 Oct 2025 | Prob (F-statistic): | 0.00471 |
| Time: | 13:17:56 | Log-Likelihood: | 9.5354 |
| No. Observations: | 10 | AIC: | -13.07 |
| Df Residuals: | 7 | BIC: | -12.16 |
| Df Model: | 2 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 1.5570 | 0.035 | 44.177 | 0.000 | 1.474 | 1.640 |
| height | 0.1285 | 0.051 | 2.503 | 0.041 | 0.007 | 0.250 |
| diameter | 0.0736 | 0.051 | 1.433 | 0.195 | -0.048 | 0.195 |
| Omnibus: | 0.195 | Durbin-Watson: | 1.779 |
|---|---|---|---|
| Prob(Omnibus): | 0.907 | Jarque-Bera (JB): | 0.363 |
| Skew: | -0.202 | Prob(JB): | 0.834 |
| Kurtosis: | 2.159 | Cond. No. | 2.34 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
結果として、高さにかかる回帰係数が直径よりも大きいことが確認されました。つまり、コナラのどんぐりの場合は、重さに対して高さがより強い影響を与えていると考えられます。
8.4.3. 変数選択#
回帰分析において、モデルに複数の説明変数を含めることは可能ですが、変数が多くなればなるほど必ずしも良いモデルが得られるわけではありません。過剰な変数の追加は、モデルが過剰適合(overfitting)する原因となることもあります。したがって、回帰分析を行う際には、複数の変数を様々な組み合わせでモデル化し、その中から最適なモデルを選択する作業が必要です。
統計分野でモデルの良さを測る指標として一般的に使用されているのが赤池情報量基準(Akaike’s information criterion; AIC)です。AIC は、モデルの適合性と複雑さ(変数の数)とのバランスを取るために使われます。AIC が小さいほど、より良いモデルとされます。
クヌギのデータを利用して、どんぐりの高さのみを使って重さを説明するモデルを構築し、その AIC を計算します。
acorns_data = pd.read_csv('acorns.clean.csv')
kunugi = acorns_data.loc[acorns_data['tree'] == 'kunugi', ]
X = kunugi['height']
y = kunugi['weight']
m1 = sm.OLS(y, sm.add_constant(X))
r1 = m1.fit()
r1.aic
np.float64(16.079093773259917)
次に、重さを直径で説明するモデル、そして重さを高さと直径の両方を使って説明するモデルの AIC も計算します。
X = kunugi['diameter']
y = kunugi['weight']
m2 = sm.OLS(y, sm.add_constant(X))
r2 = m2.fit()
r2.aic
np.float64(5.063185098820146)
X = kunugi[['height', 'diameter']]
X = (X - X.mean()) / X.std()
y = kunugi['weight']
m3 = sm.OLS(y, sm.add_constant(X))
r3 = m3.fit()
r3.aic
np.float64(-0.2973567786079414)
これらの結果を比較すると、最も AIC が低いのは、高さと直径の両方を説明変数としたモデルであることがわかります。つまり、このデータセットにおいては、どんぐりの重さを説明するためには、高さと直径の両方を含めたモデルが最適であると言えます。実際、どんぐりは一般に大きくなるほど重くなると推察され、高さおよび直径が大きさを反映しているとすれば、この結果は統計的にも直感的にも妥当と言えるでしょう。
もっとも、今回の分析に使ったデータは、筆者が虫喰いどんぐりを丁寧に取り除き、さらに「外れ値」という名の不都合な真実もそっと隠し持ちつつ測定しています。教材だからできる特権ですが、現実のどんぐりはそう簡単に協力してくれません。現実のどんぐりたちは、もっと複雑なドラマを繰り広げているに違いありません。
このように最適なモデルを選ぶ過程は、モデル選択(model selection)または変数選択(variable selection)と呼ばれ、回帰分析において重要なステップです。上記の例では、考えられる説明変数の組み合わせすべてで回帰モデルを作成し、最適なモデルを選びました。この方法は総当たり法などとも呼ばれています。
説明変数が 2 つの場合は、組み合わせは 3 通り(height、diameter、height + diameter)だけ試せばよいですが、説明変数が増えると組み合わせ数は急激に増加します。そのため、このような場合には変数増加法や変数減少法、スパース回帰などの手法を使うことが一般的です。また、ランダムフォレストなどの機械学習アルゴリズムも変数選択に役立つ方法です。

