4.2. 繰り返し構文#
世界は繰り返しでできています。太陽が昇り、沈み、また昇る。リスはどんぐりを埋め、忘れ、また埋める。プログラムにも同じく、繰り返しの作業を効率よく処理するための仕組みが必要です。それが繰り返し構文(ループ構文)です。Python には主に 2 種類あり、for と while があります。使い分けると効率的ですが、基本的にはどちらも同じ処理を書くことができます。
4.2.1. for 文#
あるリストの要素の合計を計算するプログラムを作ることで、繰り返し処理の基本を見ていきましょう。まず、次のように数値が入ったリストを用意します。
x = [2, 3, 1, 5, 10]
Python にはリストの合計を求めるための便利な関数 sum がありますが、ここでは繰り返し構文を使って自分で合計を計算する方法を考えましょう。図のように、変数 i を用意し、i の値を 0、1、2、…と変えながら、リスト x の各要素 x[i] を変数 s に足していきます。こうすることで、最後にはリストのすべての要素の合計が s に入ります。
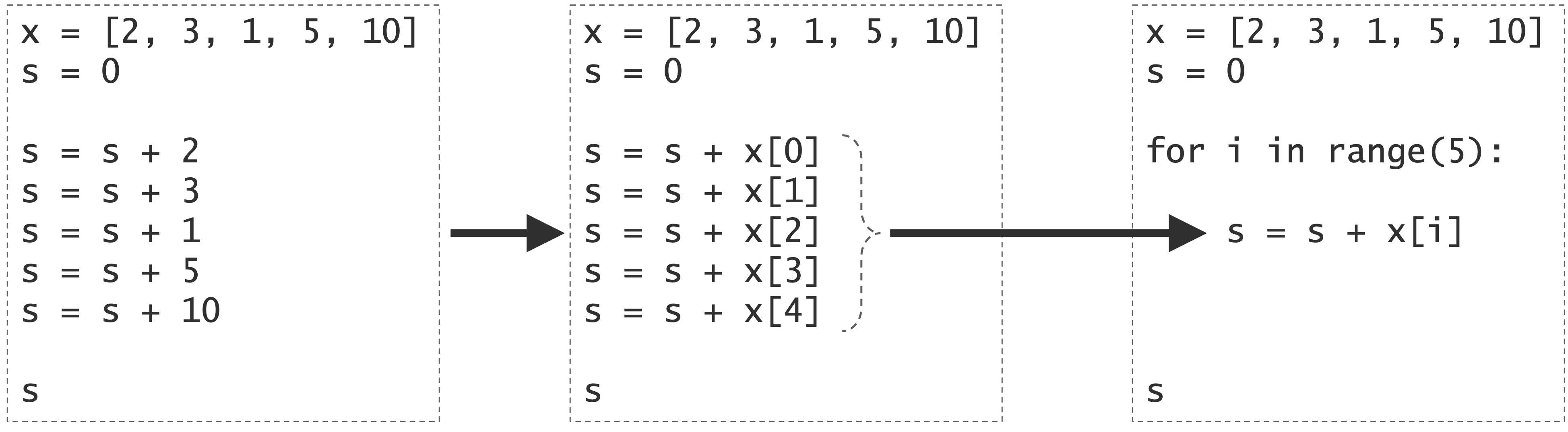
Fig. 4.1 for 文を利用してリスト要素の合計を計算する手順。#
このように、i を順に変化させるには、for と range 関数を組み合わせて使います。まずは、for と range の組み合わせだけを使った簡単な例を見てみましょう。
for i in range(5):
print(i)
0
1
2
3
4
このプログラムでは、range(5) が 0 から 4 までの 5 つの整数を順に生成し、それが変数 i に代入されます。そして、print 関数によって i の値が画面に表示されます。なお、for 文の中では、print 関数を利用しない場合、変数の中身が出力されません。
これで、i が 0、1、2、3、4 と変化することが確認できたので、i をリストのインデックスとして利用し、print の代わりに変数 s に x[i] の値を順に足していく処理に書き換えてみましょう。
s = 0
for i in range(5):
s = s + x[i]
s
21
この例では、range(5) としてリストの要素数に合わせましたが、リストのサイズが変わるたびに数値を手動で変更するのは手間がかかります。そこで、リストの長さを自動で取得できる len 関数を使うと便利です。
s = 0
for i in range(len(x)):
s = s + x[i]
s
21
次に、別の視点から for 文の使い方を見ていきましょう。先ほどの例では、for i in range(5) と書き、range(5) が生成する 0、1、2、3、4 を順に変数 i に代入し、その i を使ってリスト x の各要素を取得していました。
Python では、リストのインデックスを使わずに、直接リストの各要素を取り出して繰り返し処理を行うこともできます。この場合、for m in x と書くと、リスト x の要素が順に変数 m に代入されます。実際に試してみましょう。
for m in x:
print(m)
2
3
1
5
10
このコードでは、リスト x の各要素(2、3、1、5、10)が順に変数 m に代入され、それぞれ print(m) によって表示されます。リストの要素の合計を求める場合も、この方法が使えます。次のように書くと、m にリスト x の各要素が順番に代入され、それらを変数 s に足し合わせることで合計を計算できます。
s = 0
for m in x:
s = s + m
s
21
このように for 文の使い方には、大きく分けて 2 通りの方法があります。ひとつはリストのインデックスを使う方法で、連続した整数のリストを生成し(range(len(x)))、それを使ってリスト x の各要素にアクセスする方法です。もうひとつはリストの要素を直接扱う方法で、リスト x に対して繰り返し処理を行い、各要素を順に変数に代入して操作します(for m in x)。どちらの方法でも、リストの全要素に対して繰り返し処理を行うことができます。
次に、for 文を使った少し複雑な計算例として、リストの要素の平均を計算する方法を見てみましょう。平均を求めるには、リストの要素の合計だけでなく、要素の個数も必要になります。そこで、for 文の中で要素の合計と個数を同時に計算する処理を書きます。
x = [2, 4, 6, 8]
s = 0
n = 0
for m in x:
s = s + m
n = n + 1
ave = s / n
ave
5.0
このように for 文の中に必要なだけの処理を追加することも可能です。
次に、for 文と if 文を組み合わせた例を見ていきましょう。for 文の中に if 文を入れることで、いわゆる「入れ子構造」を作ることができます。このとき、for 文と if 文のインデントの位置に注意しましょう。正しくインデントしないと、意図した動作にならなかったりエラーになったりします。
リストの中から奇数の個数を数えるプログラムを作成してみます。
x = [1, 2, 3, 4, 5, 6, 7, 8, 9]
n = 0
for m in x:
if m % 2 == 1:
n = n + 1
n
5
上の例と同様に、リストの中にある 3 の倍数の個数を数えるプログラムを作ってみましょう。
3 の倍数かどうかを判定するときには、「0 より大きい」ことと「3 で割った余りが 0 である」という二つの条件を同時に満たしている必要がある点に注意してください。この条件の書き方は、if 文を二重に重ねて入れ子にしてもよいですし、論理演算子の and を使って一つの if 文にまとめても構いません。
x = [1, 2, 3, 4, 5, 6, 7, 8, 9]
n = 0
Show code cell content
n = 0
for m in x:
if m > 0:
if m % 3 == 0:
n = n + 1
n
3
Show code cell content
n = 0
for m in x:
if (m > 0) and (m % 3 == 0):
n = n + 1
n
3
練習問題 SL-1
リスト x が与えられたとき、x の要素のうち、奇数である要素の和を計算するプログラムを書きなさい。
x = [1, 2, 3, 4, 5, 6, 7, 8, 9]
s = 0
print(s)
練習問題 SL-2
リスト x が与えられたとき、x の要素のうち、奇数である要素の平均値を計算するプログラムを書きなさい。
x = [1, 2, 3, 4, 5, 6, 7, 8, 9]
ave = 0
print(ave)
練習問題 SL-3
正の整数が与えられたとき、その整数の約数をリストに保存するプログラムを作成してください。例えば 6 が与えられた場合、1, 2, 3, 6 を含むリストが作られます。
n = 6
divisors = []
print(divisors)
もう一つの例として、素数の判定プログラムを書いてみましょう。素数とは、1 とその数自身以外で割り切れない整数のことです。ここでは、整数 n が与えられたとき、n が素数であれば is_prime に True を、素数でなければ False を代入するプログラムを作ってみましょう。
考え方として、以下の手順をとります。
nの約数を保存するためのリストn_divisorsを作ります。kを1からnまで変化させ、次の処理を行います。nがkで割り切れる場合、kをn_divisorsに追加します。n_divisorsに含まれている数が1とnだけであれば、is_primeにTrueを代入します。
Show code cell content
n = 1123
n_divisors = []
is_prime = False
for k in range(n):
k = k + 1
if n % k == 0:
n_divisors.append(k)
if len(n_divisors) == 2:
if (n_divisors[0]) == 1 and (n_divisors[1] == n):
is_prime = True
is_prime
True
ここで使われている True と False は、Python において特別な意味を持つ値です。プログラムで真偽判定を行うと、その結果は「真(True)」か「偽(False)」のいずれかになります。このように、論理的な真偽を表す値として True と False が用意されています。
次に、for 文の入れ子構造を活用して、もう少し複雑なプログラムを書いてみましょう。先ほどの素数判定プログラムを応用し、ある数 m 以下のすべての素数を見つけて、それらをリスト primes に保存するように修正します。これにより、1 から m までの整数を順に調べ、それぞれが素数かどうかを判定し、素数ならばリストに追加していく処理が実現できます。
手順としては、以下のようになります。
m以下の素数を保存するためのリストprimesを作ります。nを1からmまで変化させ、次の処理を行います。nの約数を保存するためのリストn_divisorsを作ります。kを1からnまで変化させ、次の処理を行います。nがkで割り切れる場合、kをn_divisorsに追加します。
n_divisorsに含まれている数が1とnだけであれば、nをprimesに追加します。
このように、外側の for 文で n を 1 から m まで繰り返し、各 n に対して素数判定を行うことで、m 以下のすべての素数を探し出せます。
m = 100
primes = []
for n in range(m):
n = n + 1
n_divisors = []
for k in range(n):
k = k + 1
if n % k == 0:
n_divisors.append(k)
if len(n_divisors) == 2:
if (n_divisors[0]) == 1 and (n_divisors[1] == n):
primes.append(k)
primes
[2,
3,
5,
7,
11,
13,
17,
19,
23,
29,
31,
37,
41,
43,
47,
53,
59,
61,
67,
71,
73,
79,
83,
89,
97]
練習問題 SL-4
完全数(perfect number)とは、自分自身を除く正の約数の和が自分自身に等しくなる自然数のことであす。たとえば、
6 = 1 + 2 + 3
28 = 1 + 2 + 4 + 7 + 14
496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248
が完全数です。正の整数が与えられたとき、その整数は完全数かどうかを判定するプログラムを作成してください。
n = 28
is_pn = None
print(is_pn)
長さが同じリストを複数同時に for 文で処理したい場合は、for i in range(len(x)) のように、片方のリストを使ってインデックス i を生成し、それを複数のリストに適用することで実現できます。たとえば、次のように書きます。
trees = ['kunugi', 'arakashi', 'shirakshi']
weights = [5.56, 1.43, 1.68]
for i in range(len(trees)):
print(trees[i], weights[i])
kunugi 5.56
arakashi 1.43
shirakshi 1.68
また、複数のリストの値を一時変数に代入して繰り返し処理を行いたい場合は、zip 関数を使います。繰り返し対象のリストを zip 関数に渡すと、それぞれのリストから順に 1 要素ずつ取り出してくれます。
trees = ['kunugi', 'arakashi', 'shirakshi']
weights = [5.56, 1.43, 1.68]
for tree, weight in zip(trees, weights):
print(tree, weight)
kunugi 5.56
arakashi 1.43
shirakshi 1.68
どんぐりを 1 つずつ数えていたリスも、今では for 文で高速集計中。if 文と組み合わせれば、美味しいどんぐりだけを選び出すこともできます。とはいえ、リス本人は「美味しい」の基準がその日の気分で変わることに気づいていません。
4.2.2. while 文#
繰り返し処理には、for 文のほかに while 文もあります。for 文は、繰り返す回数や範囲があらかじめ決まっている場合に使うのが特徴です。一方で、while 文は、ある条件が成立している間だけ処理を繰り返すという特徴があります。得意とする場面は異なりますが、基本的にはどちらも同じ処理を書くことができるため、初心者は覚えやすい方をまず一つ身につけるとよいでしょう。
リストの要素の合計を計算するプログラムを while 文で書いてみましょう。
x = [2, 4, 6, 8]
s = 0
i = 0
while i < len(x):
s = s + x[i]
i = i + 1
s
20
次に、素数判定プログラムも while 文を使って書いてみましょう。
n = 1123
n_divisors = []
is_prime = False
k = 0
while k < n:
k = k + 1
if n % k == 0:
n_divisors.append(k)
if len(n_divisors) == 2:
if (n_divisors[0]) == 1 and (n_divisors[1] == n):
is_prime = True
is_prime
True
for 文があらかじめ繰り返し範囲を決めているのに対し、while 文は範囲が決まっていません。そのため、毎回条件を判定し、条件が成立している間は処理が続きます。この条件判定が正しくないと、繰り返し処理が永遠に続き、いわゆる「無限ループ」に陥る可能性があるため注意が必要です。たとえば、以下のように i の更新を忘れてしまうと、i はずっと 0 のままで、x[0] が無限に加算されることになり、メモリを大量に消費してシステムに負担がかかります。
x = [2, 4, 6, 8]
s = 0
i = 0
while i < len(x):
s = s + x[i]
s
練習問題 SL-5
n が与えられたとき、n 以下の最大の素数を探すプログラムを while 文で書きなさい。
練習問題 SL-6
ある池の表面積は 10km2(10,000,000m2)です。この池に外来植物が生息し始め、初めは池の表面積の 1m2 を覆っています。この植物が毎日倍増すると仮定して、池全体を覆うまでに要する日数を計算するプログラムを作成してください。
pond_size = 10000000
plant_area = 1
n_days = 0
print(n_days)
練習問題 SL-7
複数の要素からリストが与えられたとき、これらの要素を昇順に並べ替えるプログラムを作成してください。なお、sorted 関数やリストの sort メソッドなどを利用しないこと。
x = [2, 3, 5, 1, 4]
print(x)
「今日はどんぐりを 5 個埋める!」と決めて作業を始めたリスがいたとすれば、それは for の思考法です。終わりが見えているので、頑張る気力も湧いてきます。「疲れるまでどんぐりを埋めよう」と曖昧な目標で動き出したリスがいたら、それは while の世界。疲れの定義が曖昧なままだと、延々と埋め続ける羽目になります。
ちなみにそのリス、冬眠のタイミングを完全に見失ったそうです。
4.2.3. break#
n 以下の最大の素数を求めるには、n から 1 に向かって数をひとつずつ減らしながら、それぞれが素数かどうかを調べていく方法が考えられます。このとき、最初に見つかった素数が n 以下で最大の素数になります。
%%time
m = 100
max_prime = 0
for n in range(m):
n = m - n # change "0, 1, 2, ..., m - 1" to "m, m - 1, m - 2, ..., 1"
n_divisors = []
for k in range(n):
k = k + 1
if n % k == 0:
n_divisors.append(k)
if len(n_divisors) == 2:
if (n_divisors[0]) == 1 and (n_divisors[1] == n):
if k > max_prime:
max_prime = k
max_prime
CPU times: user 514 μs, sys: 67 μs, total: 581 μs
Wall time: 836 μs
97
このプログラムでは、100 から 1 に向かって素数を探しています。しかし、たとえば最大の素数である 97 を見つけた後も、繰り返し処理はそのまま続行され、96、95、…、1 まで無駄な判定処理が行われてしまいます。こうした不要な計算を避けるには、最初に素数を見つけた時点で for 文を終了させるように、break を使って処理を途中で打ち切るようにしましょう。
%%time
m = 100
max_prime = 0
for n in range(m):
n = m - n
n_divisors = []
for k in range(n):
k = k + 1
if n % k == 0:
n_divisors.append(k)
if len(n_divisors) == 2:
if (n_divisors[0]) == 1 and (n_divisors[1] == n):
if k > max_prime:
max_prime = k
break
max_prime
CPU times: user 106 μs, sys: 0 ns, total: 106 μs
Wall time: 110 μs
97
これで、最大の素数を見つけた時点で計算が停止し、実行時間が大幅に減少することが確認できるでしょう。このように、for 文や while 文に break 文を適切に組み合わせることで、無駄な計算処理を削減し、効率的なプログラムを作成できます。
社会には、上司が帰らない限り帰れないという条件式が永遠に真のまま続く while 文があります。break 条件は最初から抜け落ちていて、しかも誰も修正しようとしません。

