7.2. 基本グラフ#
本節では、Maptlolib を利用して折れ線グラフ、棒グラフ、ヒストグラム、散布図、箱ひげ図などの基本的なグラフを描く方法を紹介します。
グラフの可視化に使用するデータセットについて、ここで紹介します。まず、どんぐりのデータセット(acorns.clean.csv)には、さまざまな種類のどんぐり(樹種)に関する情報が記録されています。各サンプルについて、樹種(tree)、重さ(weight)、高さ(height)、直径(diameter)のデータが記録されています。
# !wget https://py.biopapyrus.jp/data/acorns.clean.csv
acorn_data = pd.read_csv('acorns.clean.csv')
acorn_data.head()
| tree | weight | height | diameter | |
|---|---|---|---|---|
| 0 | kunugi | 5.55 | 2.27 | 1.89 |
| 1 | kunugi | 4.62 | 1.98 | 1.84 |
| 2 | kunugi | 5.05 | 2.08 | 1.90 |
| 3 | kunugi | 5.44 | 2.18 | 1.91 |
| 4 | kunugi | 5.60 | 2.20 | 1.93 |
次に、遺伝子発現量データ(cinsueta_exp.csv)は、タネツケバナの一種である Cardamine insueta の葉を水面に浮かべたあと、経過時間(0〜96時間)ごとの遺伝子発現量の変化を測定したデータです。
# !wget https://py.biopapyrus.jp/data/cinsueta_exp.csv
exp_data = pd.read_csv('cinsueta_exp.csv', index_col=0)
exp_data.head()
| 0h | 2h | 4h | 8h | 12h | 24h | 48h | 72h | 96h | |
|---|---|---|---|---|---|---|---|---|---|
| gene | |||||||||
| CARHR000010 | 419 | 306 | 1935 | 2310 | 2976 | 242 | 543 | 739 | 402 |
| CARHR000060 | 531 | 149 | 981 | 70 | 123 | 348 | 691 | 366 | 160 |
| CARHR000090 | 27 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| CARHR000110 | 108 | 30 | 93 | 101 | 127 | 55 | 98 | 99 | 75 |
| CARHR000120 | 14 | 5 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
7.2.1. 散布図#
散布図は二つの連続値データ同士の関係性を図示するグラフである。データの範囲が大きい場合は、縦軸、横軸または両方を対数化して描くことで、二つの変数の関係性が見やすくなることがあります。対数化は、自然対数 loge や常用対数 log10 のどちらを使ってもよいが、log10 を利用することで、実際の数値の桁数が反映されているため、生物や農学の分野でよく使われます。また、生物学において、遺伝子発現量などで倍増などのように 2 の倍数に着目する場合、log2 もよく利用されています。
散布図は scatter メソッドを利用して描きます。引数として、横軸と縦軸の座標を与えます。たとえば、どんぐりのデータセットを読み込み、どんぐりの高さと重さの関係を可視化してみましょう。
x = acorn_data['height']
y = acorn_data['weight']
fig = plt.figure()
ax = fig.add_subplot()
ax.scatter(x, y)
ax.set_xlabel('height [cm]')
ax.set_ylabel('weight [g]')
plt.show()
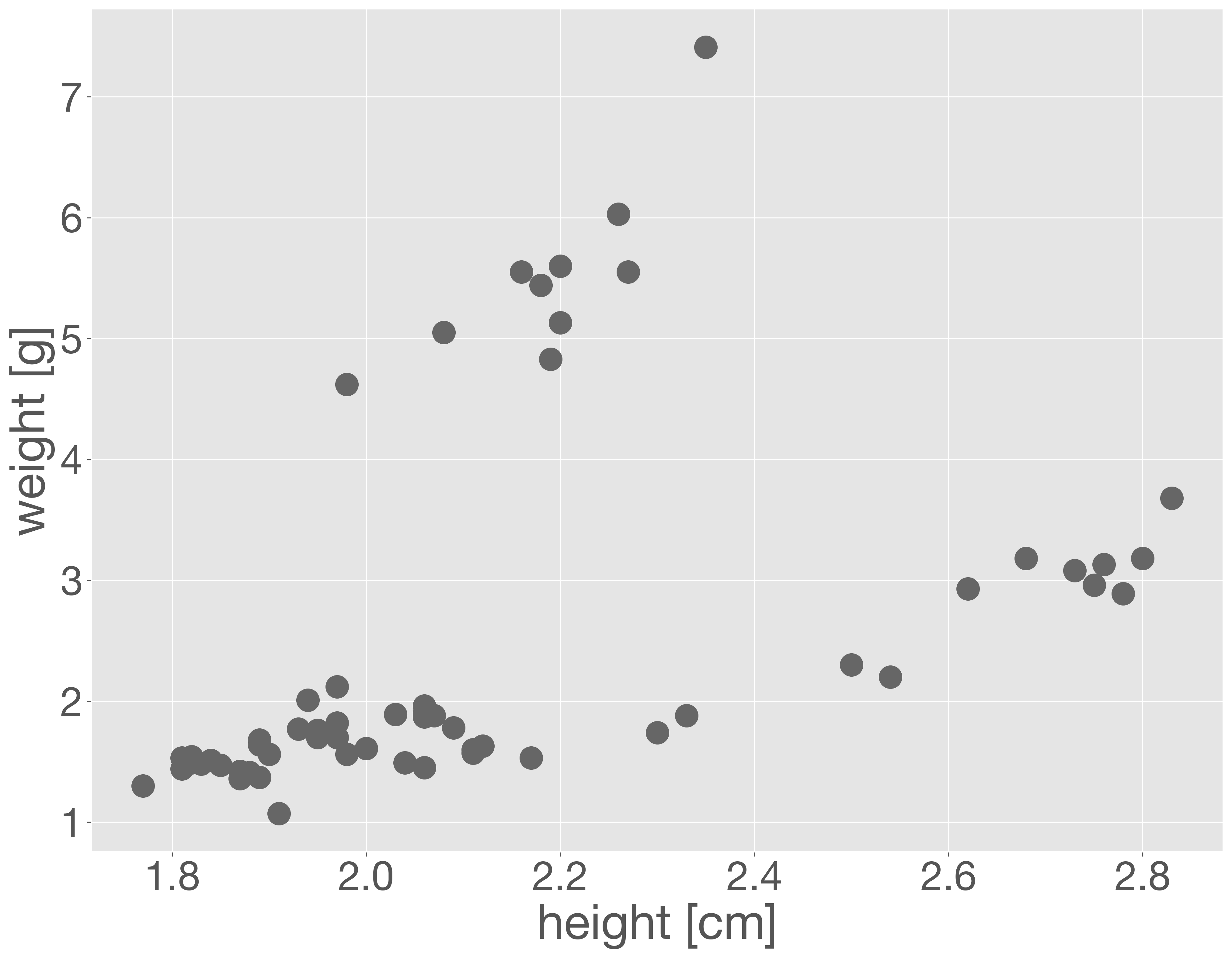
この例では、実際に散布図を描画しているのは ax.scatter の部分です。それ以前のコードは、描画デバイスや座標軸などのオブジェクトを準備している段階にあたります。また、ax.set_xlabel と ax.set_ylabel は、それぞれ横軸と縦軸のラベルを設定するために用いられています。
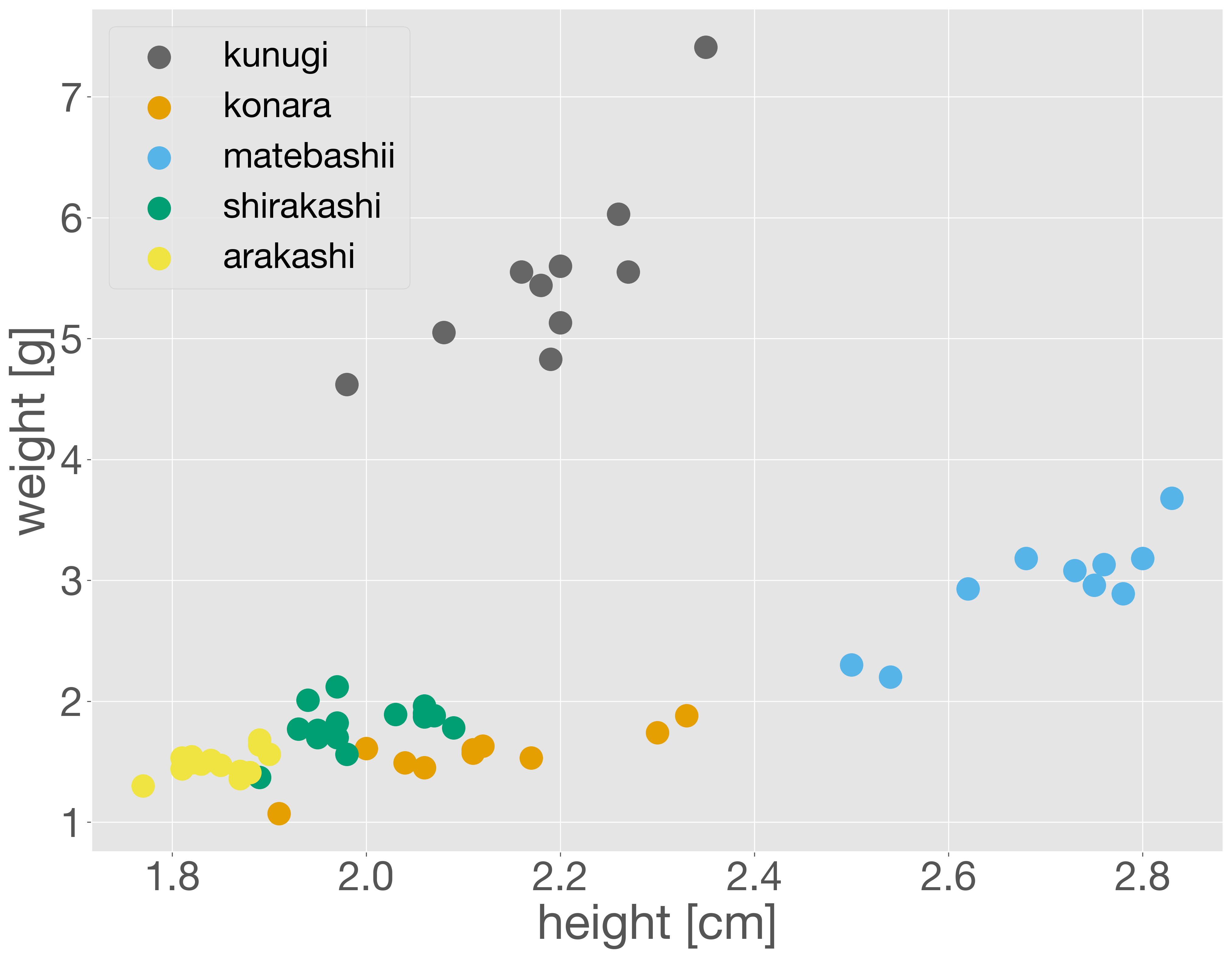
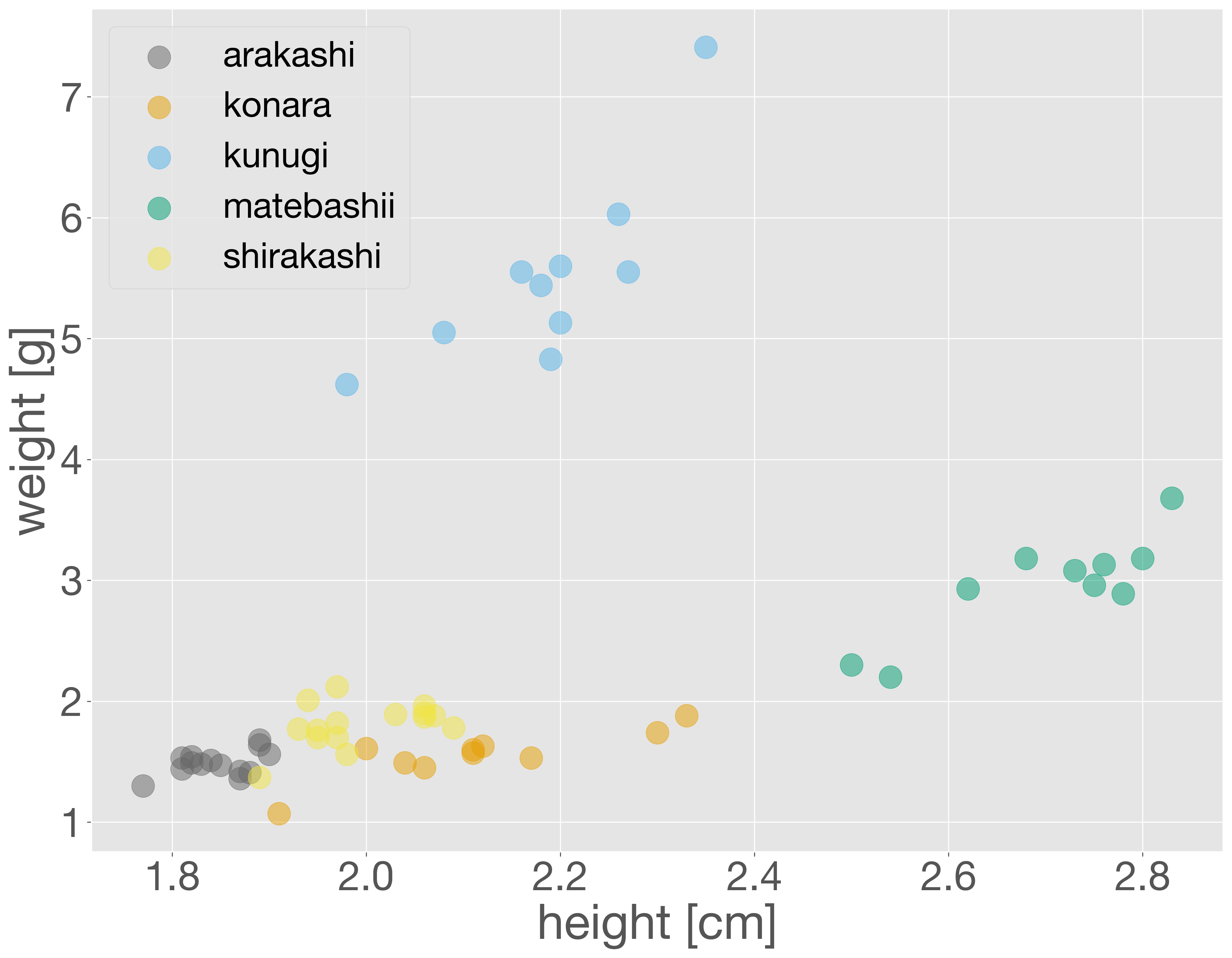
どんぐりのデータセットには、重さや高さだけでなく、どの木から落ちたかを示す tree 列も含まれています。そこで、散布図において、木の種類ごとに点の色を変えて表示してみましょう。
scatter メソッドには label オプションが用意されており、これにカテゴリ名を指定することで、各点がどのカテゴリに属するのかを示すことができます。たとえば、以下のように for 文を使って、樹種ごとに散布図を描画し、その際に label に木の名前を指定します。scatter を複数回実行することで、1 つの描画領域に複数の散布図を重ねることができます。
fig = plt.figure()
ax = fig.add_subplot()
for tree in acorn_data['tree'].unique():
x = acorn_data['height'][acorn_data['tree'] == tree]
y = acorn_data['weight'][acorn_data['tree'] == tree]
ax.scatter(x, y, label=tree)
ax.set_xlabel('height [cm]')
ax.set_ylabel('weight [g]')
ax.legend(loc='upper left')
plt.show()
なお、点の数が多く重なって見づらくなる場合は、scatter メソッドの alpha オプションを使って透明度を調整すると、グラフが見やすくなります。たとえば、alpha=0.5 と指定すると、点が半透明になります。
fig = plt.figure()
ax = fig.add_subplot()
for tree in acorn_data['tree'].unique():
x = acorn_data['height'][acorn_data['tree'] == tree]
y = acorn_data['weight'][acorn_data['tree'] == tree]
ax.scatter(x, y, label=tree, alpha=0.5)
ax.set_xlabel('height [cm]')
ax.set_ylabel('weight [g]')
ax.legend(loc='upper left')
plt.show()
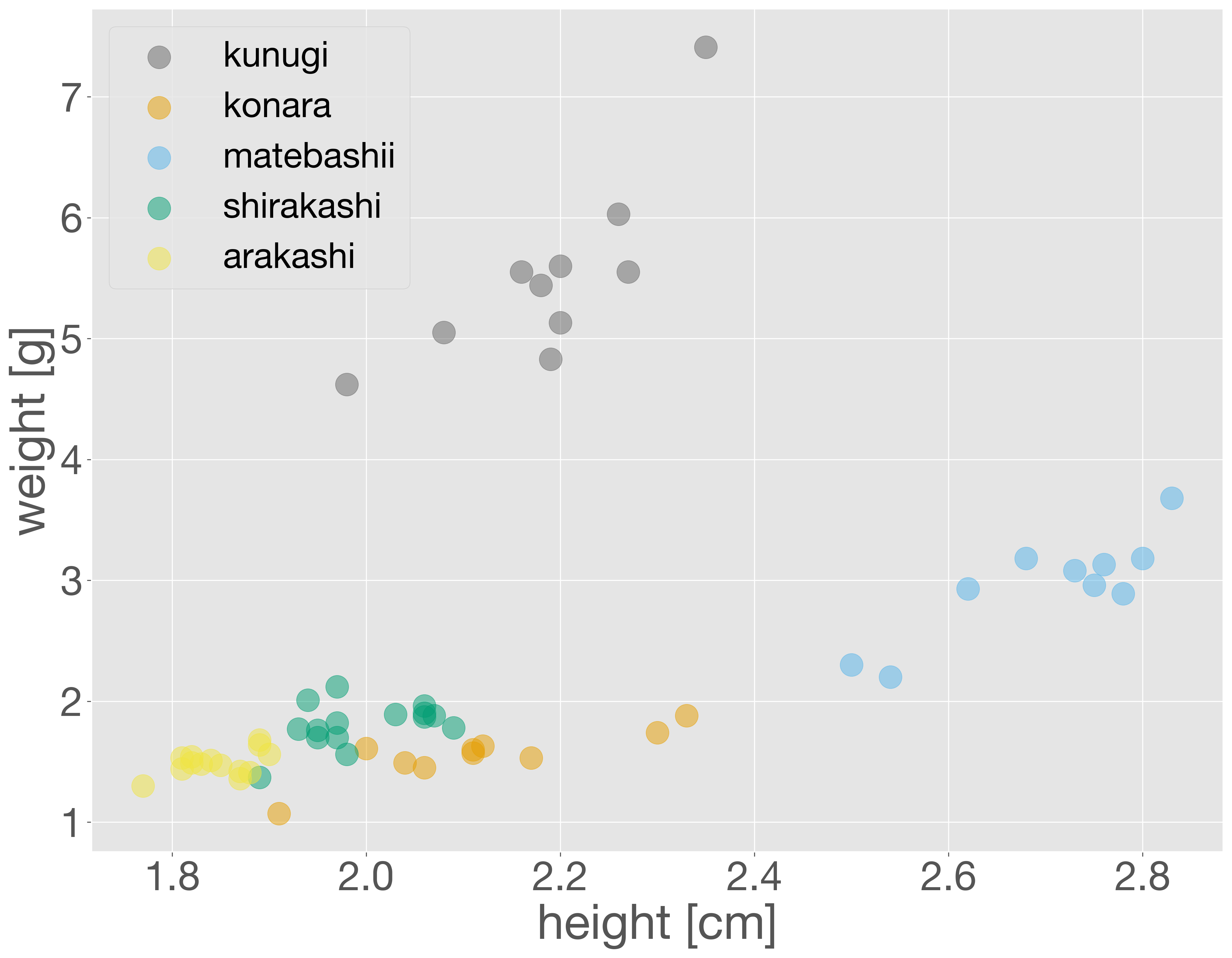
データが Pandas のデータフレーム型である場合は、groupby メソッドを使って、集計やグループごとの処理を簡潔に記述できます。それでは、上のコードを groupby を使った形に書き換えてみましょう。
Show code cell content
fig = plt.figure()
ax = fig.add_subplot()
for subset_name, subset in acorn_data.groupby('tree'):
ax.scatter(subset['height'], subset['weight'], label=subset_name, alpha=0.5)
ax.set_xlabel('height [cm]')
ax.set_ylabel('weight [g]')
ax.legend(loc='upper left')
plt.show()
問題 VC-1
acorns.clean.csv データを読み込み、「weight」と「height と diameter の積」の関係を散布図で分かりやすく図示してください。
7.2.2. 折れ線グラフ#
折れ線グラフは、連続的な数値データの変化を時系列や特定の順序に沿って可視化するのに適したグラフです。たとえば、栽培日数の経過に伴う作物の草丈の成長や、ストレス処理後における時間経過に応じた遺伝子発現量の変化などを可視化する際によく用いられます。また、データの分布やスケールの特性によっては、縦軸を対数スケール(たとえば log10)に変換して表示することで、変化の傾向をより分かりやすくすることができます。
ここでは、遺伝子発現量データセットを使って、折れ線グラフの基本的な描き方を紹介します。折れ線グラフには plot メソッドを使用します。scatter メソッドの使い方と同じです。
gene = 'CARHR000010'
x = [0, 2, 4, 8, 12, 24, 48, 72, 96]
y = np.log10(exp_data.loc[gene, :])
fig = plt.figure()
ax = fig.add_subplot()
ax.plot(x, y)
ax.set_xlabel('treatment [hour]')
ax.set_ylabel('gene expression [log10(exp)]')
plt.show()
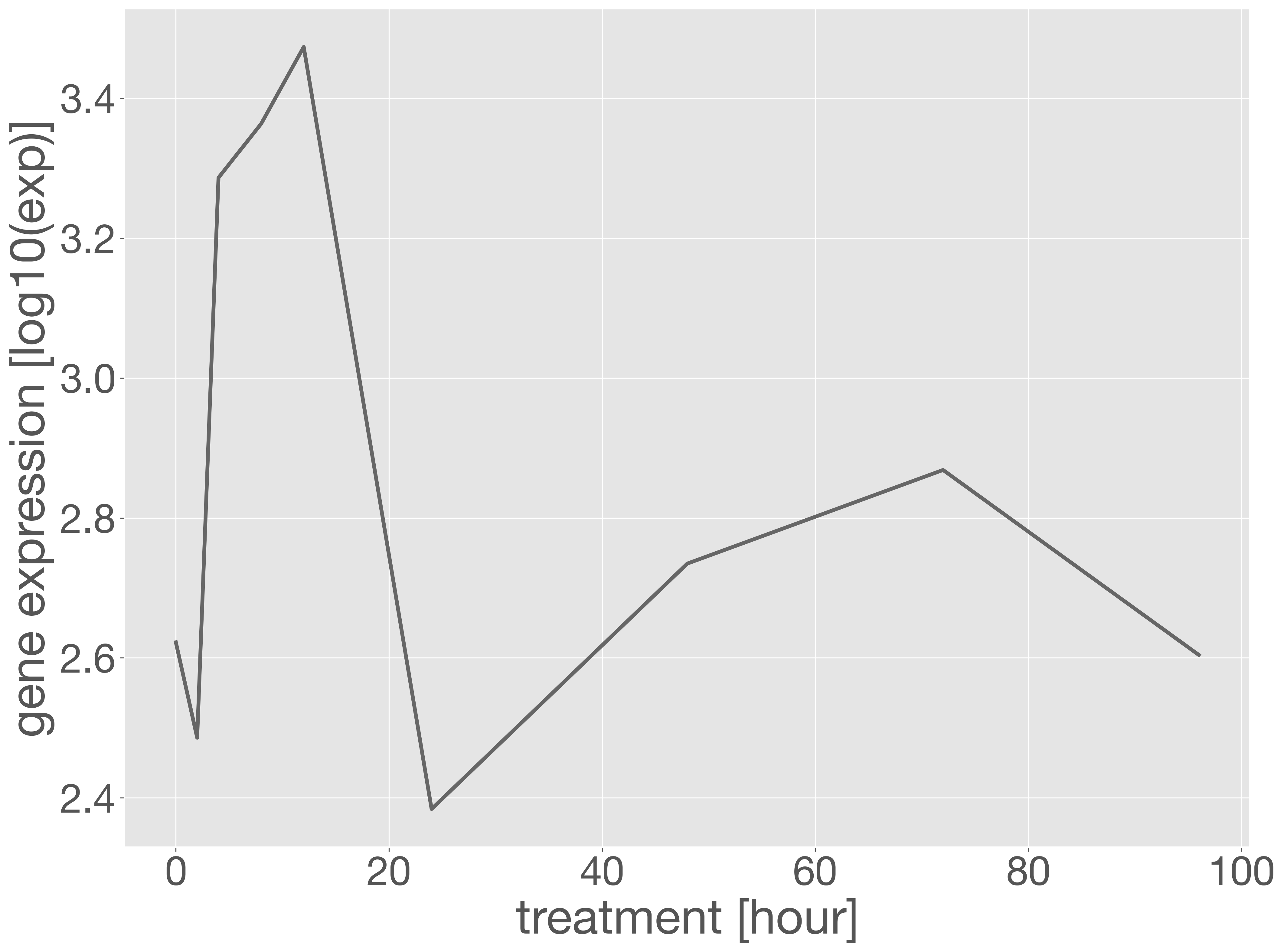
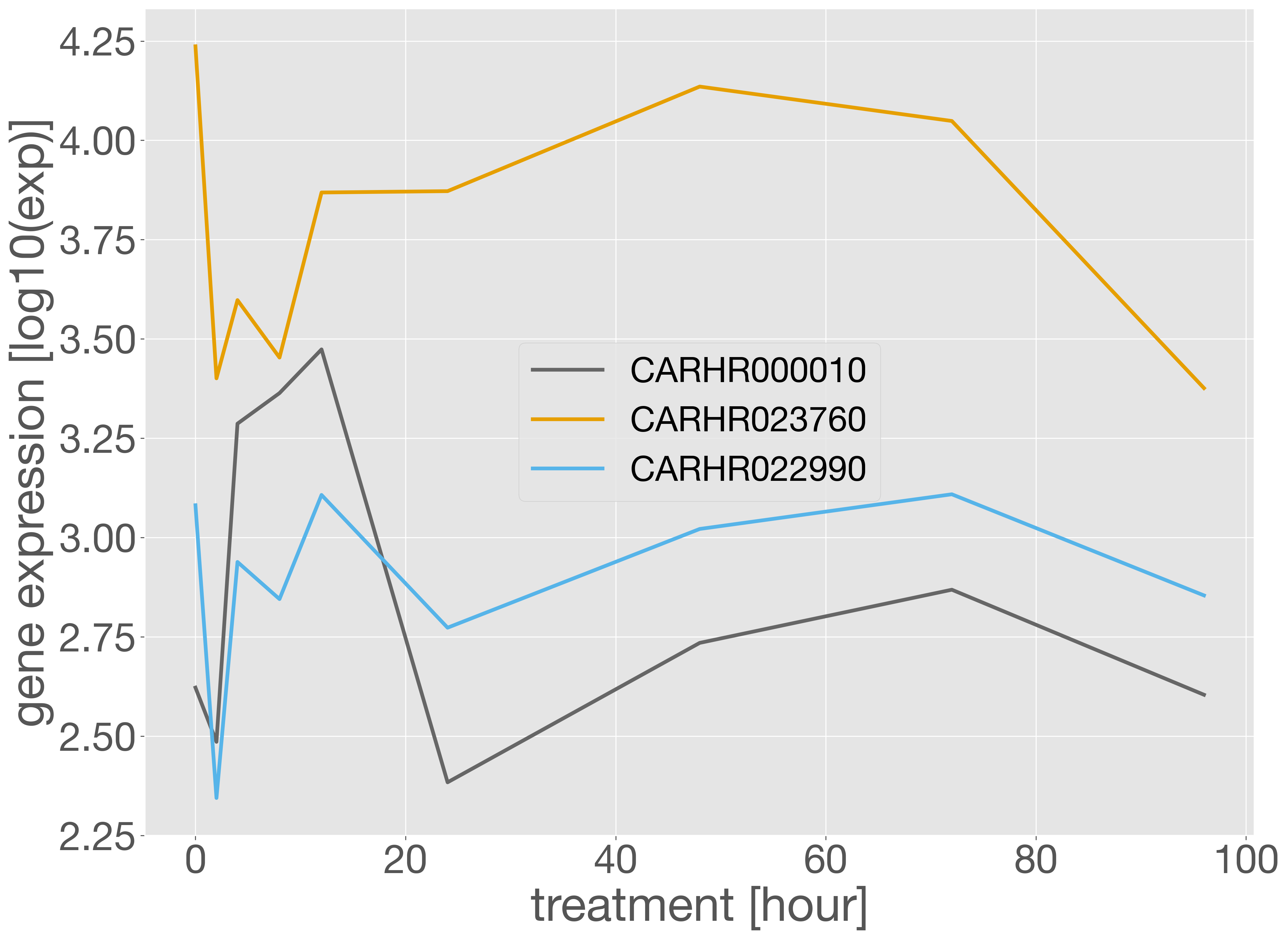
複数の遺伝子について同じグラフ上に線を描画する場合は、各遺伝子に対して plot メソッドを個別に呼び出します。その際に、label オプションに遺伝子名を指定することで、凡例を追加でき、どの線がどの遺伝子を示しているのかを明確にすることができます。
genes = ['CARHR000010', 'CARHR023760', 'CARHR022990']
fig = plt.figure()
ax = fig.add_subplot()
for gene in genes:
x = [0, 2, 4, 8, 12, 24, 48, 72, 96]
y = np.log10(exp_data.loc[gene, :])
ax.plot(x, y, label = gene)
ax.set_xlabel('treatment [hour]')
ax.set_ylabel('gene expression [log10(exp)]')
ax.legend()
plt.show()
問題 VC-2
cinsueta_exp.csv データを読み込み、ストレス処理後 2 時間(2h 列)における発現量が高い上位 5 つの遺伝子を抽出してください。その後、抽出した遺伝子の発現量の時系列変化を線グラフでわかりやすく可視化してください。
7.2.3. 棒グラフ#
棒グラフは、複数のカテゴリに属する値の大小を比較したり、可視化したりするのに適したグラフです。このグラフでは、縦軸または横軸のどちらかが連続量(数値データ)、もう一方がカテゴリ(分類)になります。棒グラフは「値の比較」が目的であるため、連続量の軸(通常は縦軸)はゼロを含むように設定し、一貫したスケールを用いる必要があります。たとえば、ゼロを省略したり、絶対値と対数スケールを混在させることは避けなければなりません。
棒グラフの作成には bar メソッドを使用します。これは散布図と同様に、横軸と縦軸の値を指定するだけで簡単に描画できます。たとえば、どんぐりのデータセットを使って、各樹種ごとのどんぐりの重さの平均値を計算し、それを棒グラフで可視化する例は以下のとおりです。
acorn_weight = acorn_data.groupby('tree').agg(np.mean)
acorn_weight
| weight | height | diameter | |
|---|---|---|---|
| tree | |||
| arakashi | 1.487857 | 1.846429 | 1.162857 |
| konara | 1.557000 | 2.115000 | 1.108000 |
| kunugi | 5.521000 | 2.187000 | 1.932000 |
| matebashii | 2.953000 | 2.699000 | 1.381000 |
| shirakashi | 1.806000 | 1.994667 | 1.230000 |
x = acorn_weight.index
y = acorn_weight['weight']
fig = plt.figure()
ax = fig.add_subplot()
ax.bar(x, y)
ax.set_xlabel('tree')
ax.set_ylabel('weight [g]')
plt.show()
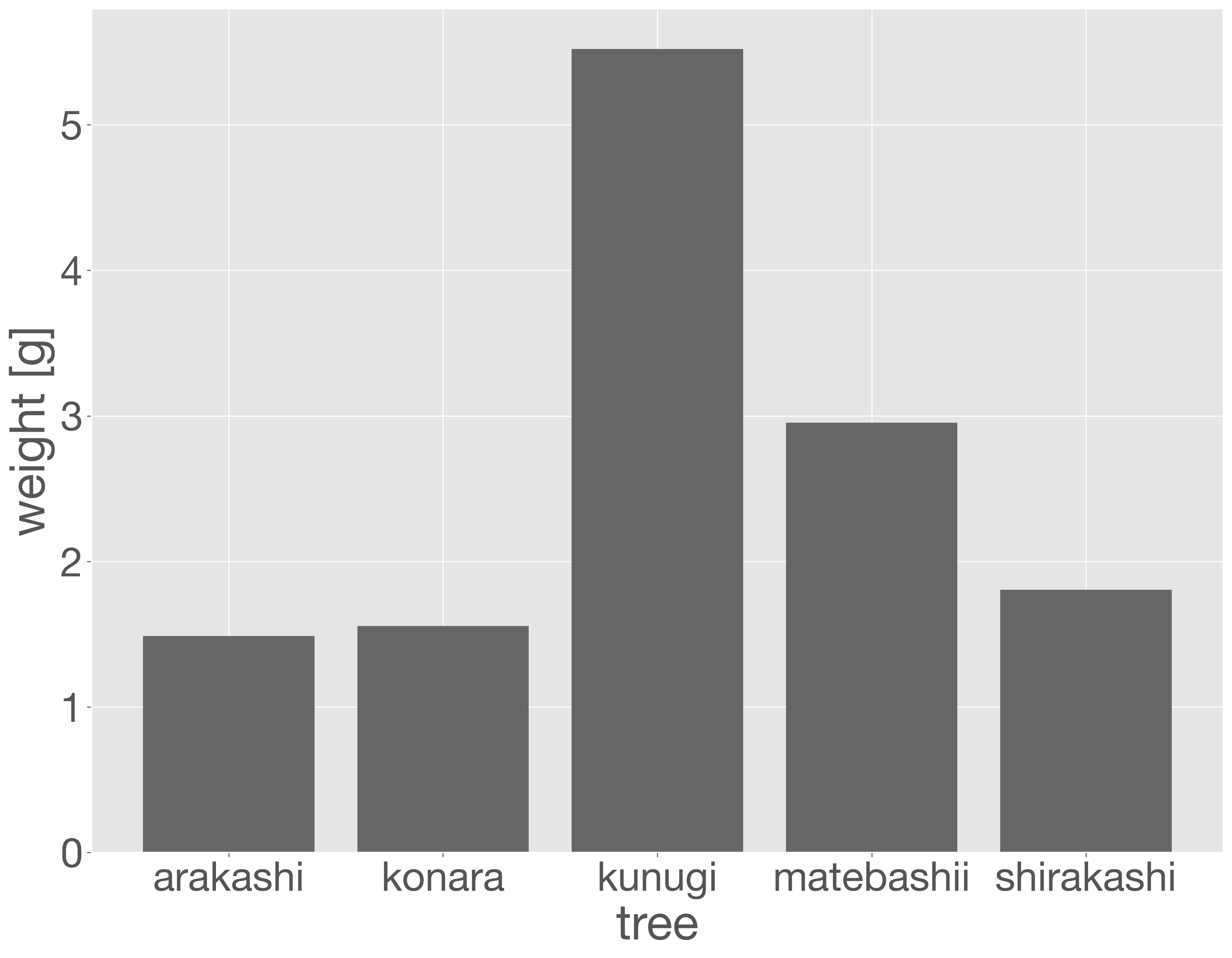
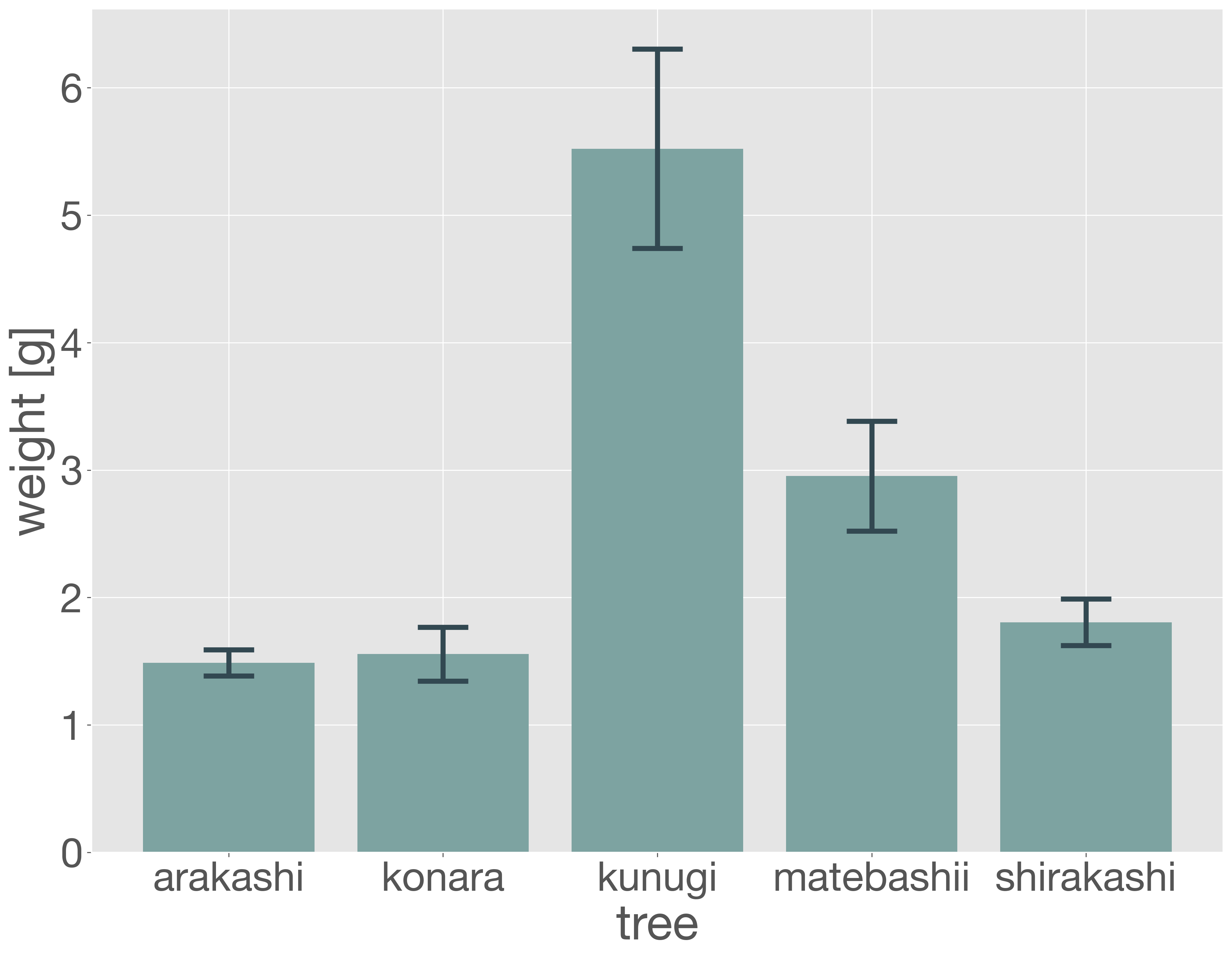
次に、エラーバー付きの棒グラフを描画してみましょう。ここでは、エラーバーとして各カテゴリにおける重さの標準偏差を表示します。これにより、平均値だけでなくデータのばらつきも視覚的に把握できるようになります。
acorn_weight = acorn_data.groupby('tree').agg([np.mean, np.std])
acorn_weight
| weight | height | diameter | ||||
|---|---|---|---|---|---|---|
| mean | std | mean | std | mean | std | |
| tree | ||||||
| arakashi | 1.487857 | 0.101994 | 1.846429 | 0.038352 | 1.162857 | 0.044623 |
| konara | 1.557000 | 0.211295 | 2.115000 | 0.127997 | 1.108000 | 0.053707 |
| kunugi | 5.521000 | 0.782154 | 2.187000 | 0.102312 | 1.932000 | 0.087152 |
| matebashii | 2.953000 | 0.431665 | 2.699000 | 0.111898 | 1.381000 | 0.090117 |
| shirakashi | 1.806000 | 0.182592 | 1.994667 | 0.061513 | 1.230000 | 0.069693 |
x = acorn_weight.index
y = acorn_weight['weight']['mean']
y_err = acorn_weight['weight']['std']
fig = plt.figure()
ax = fig.add_subplot()
ax.bar(x, y, yerr=y_err, color='#7da3a1',
error_kw={'linewidth': 4, 'capthick': 4, 'capsize': 20, 'ecolor': '#324851'})
ax.set_xlabel('tree')
ax.set_ylabel('weight [g]')
plt.show()
7.2.4. ヒストグラム#
ヒストグラムは、1 つの変数における連続値データの分布を可視化するためのグラフです。通常、横軸はデータの値をいくつかの区間(階級)に分けたもので、縦軸は各階級に属するデータの頻度(出現回数)を表します。階級の幅や数は、経験的に決めることもありますが、スタージェスの公式などのように数学的に設定することも多いです。
以下の例では、どんぐりデータセットから重さの列を取り出し、その分布をヒストグラムとして描画しています。特にオプションを指定しない場合、階級の数や幅は、データの個数や分布に応じて自動的に設定されます。
x = acorn_data['weight']
fig = plt.figure()
ax = fig.add_subplot()
ax.hist(x)
ax.set_xlabel('weight [g]')
plt.show()
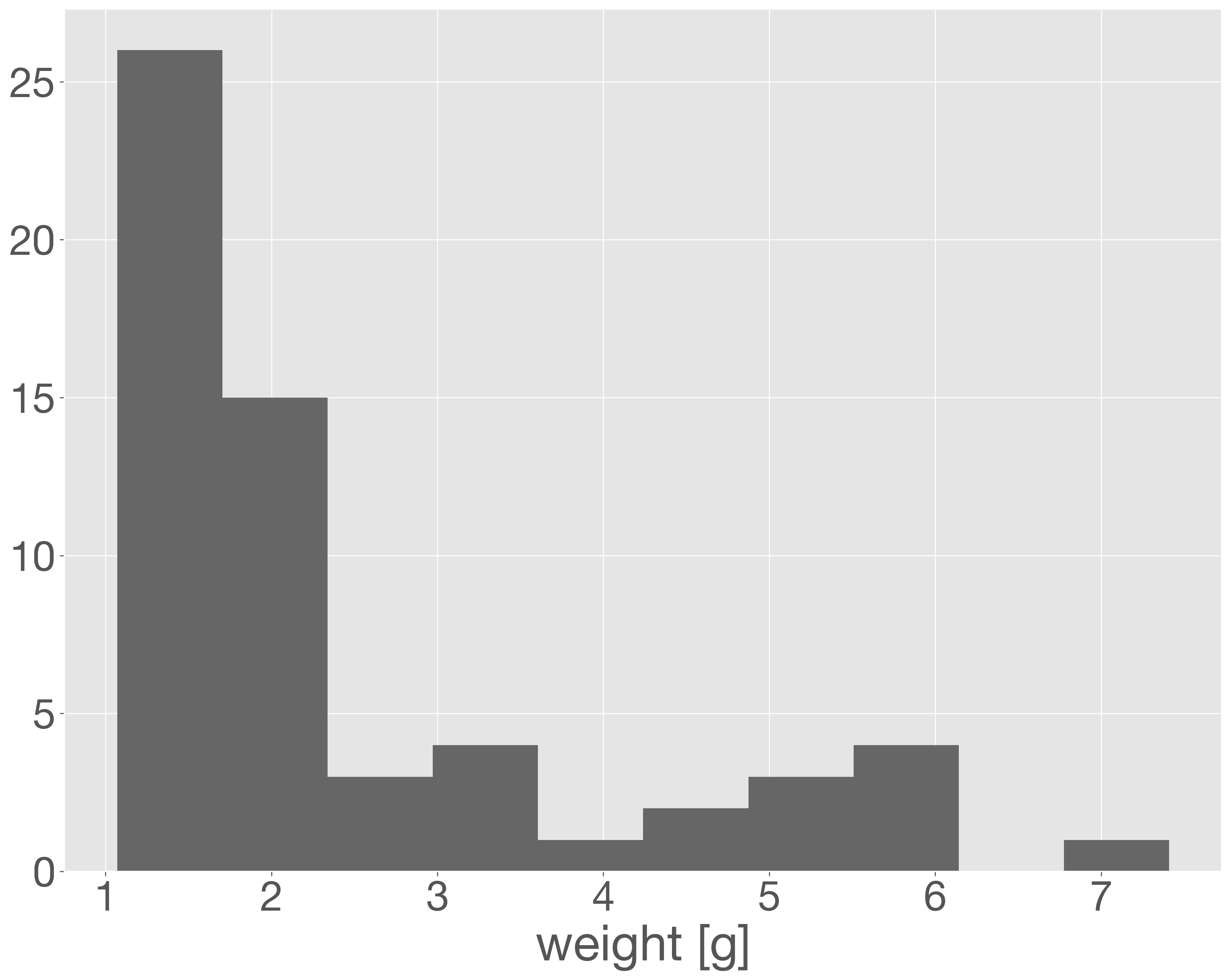
また、各樹種ごとにヒストグラムを描くこともできます。for 文を使って、樹種ごとに hist メソッドを適用することで、複数のヒストグラムを重ねて表示することができます。alpha オプションで透明度を設定すると、重なり部分が見やすくなります。
fig = plt.figure()
ax = fig.add_subplot()
for tree in acorn_data['tree'].unique():
x = acorn_data['weight'][acorn_data['tree'] == tree]
ax.hist(x, label=tree, alpha=0.8)
ax.set_xlabel('weight [g]')
ax.legend(loc='upper right')
plt.show()
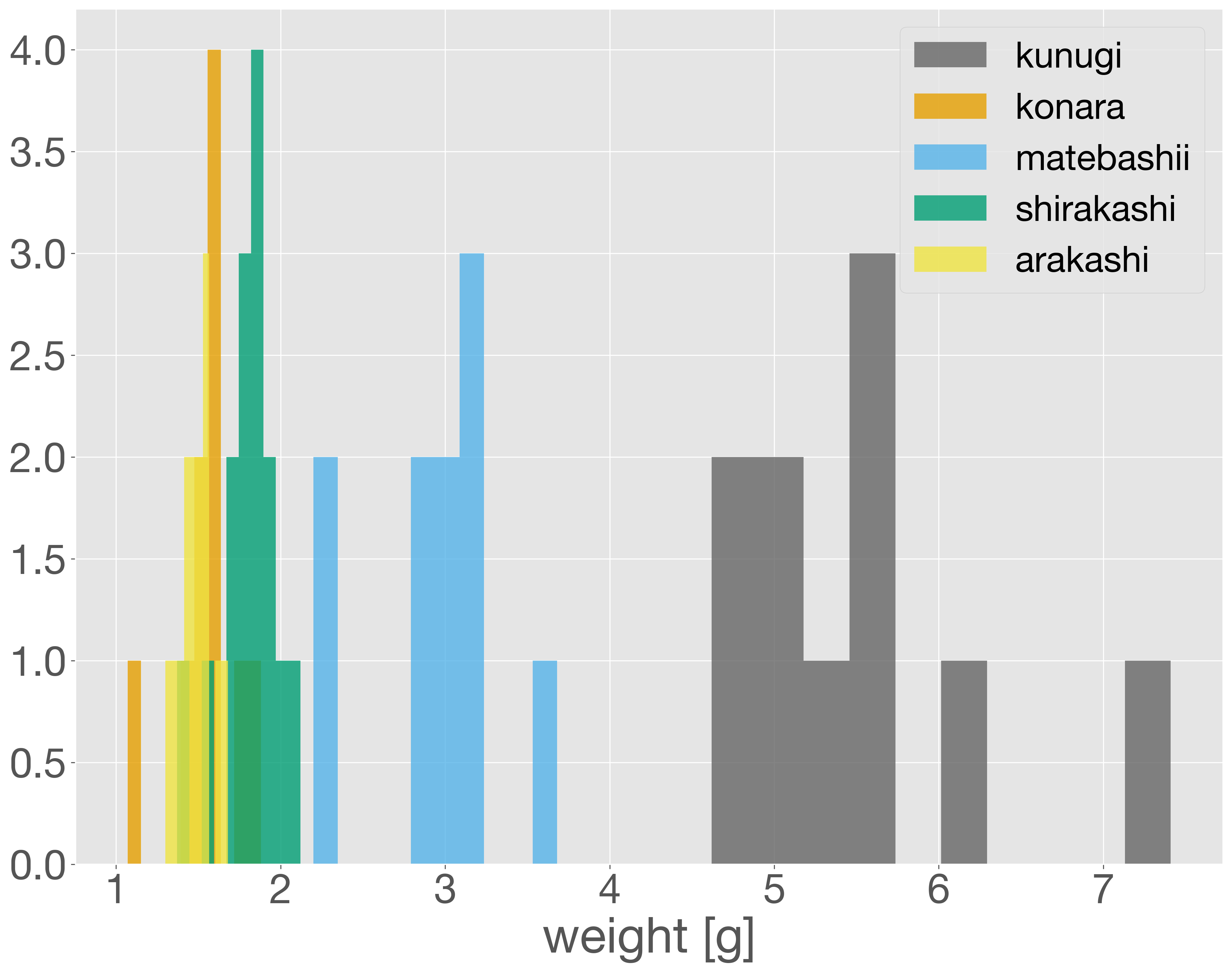
このようにヒストグラムを利用すれば、データの分布や偏りを直感的に把握することができます。
7.2.5. ボックスプロット#
ボックスプロット(箱ひげ図)は、複数の 1 変量の連続値データの分布を比較する際に有効なグラフです。ヒストグラムでは複数の分布を重ねて表示するため、比較が難しくなることがありますが、ボックスプロットを使えば、カテゴリごとに独立した位置に分布を描けるため、分布の違いを視覚的に比較しやすくなります。
ボックスプロットは、中央に箱(ボックス)と、その上下に「ひげ(線)」が伸びた図として表現されます。箱の上下端は、それぞれ第 1 四分位数(\(Q1\))と第 3 四分位数(\(Q3\))を表します。箱の中の線は中央値(第 2 四分位数)を表します。また、ひげの端は、外れ値を除いた最小値と最大値を表します。外れ値は、通常、\([Q1 - 1.5IQR, Q3 + 1.5IQR]\) の範囲外のデータとみなされ、個別にプロットされます。なお、\(IQR\) は四分位範囲のことで、\(IQR = Q3 - Q1\) と計算されます。
ボックスプロットは boxplot メソッドで描きます。縦軸のデータはリストのリスト、NumPy の配列、あるいは Pandas のデータフレームの形式で渡します。横軸のカテゴリ名(ラベル)は labels オプションで指定します。では、どんぐりのデータセットを使い、クヌギの各種測定項目をデータフレームとして、boxplot メソッドに渡し、それらの分布を可視化してみましょう。
kunugi = acorn_data.loc[acorn_data['tree'] == 'kunugi', :].iloc[:, 1:]
fig = plt.figure()
ax = fig.add_subplot()
ax.boxplot(kunugi, labels=kunugi.columns)
plt.show()
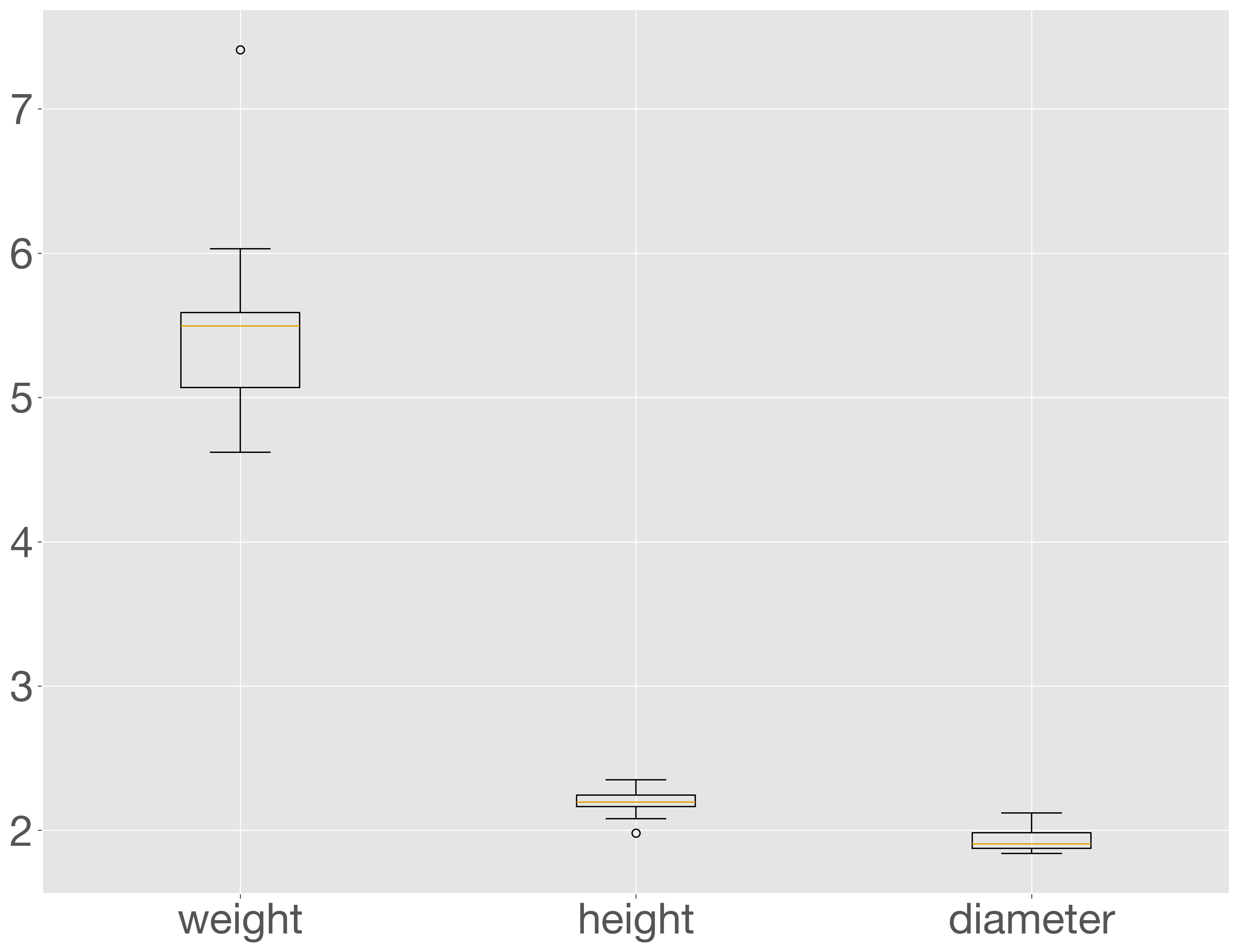
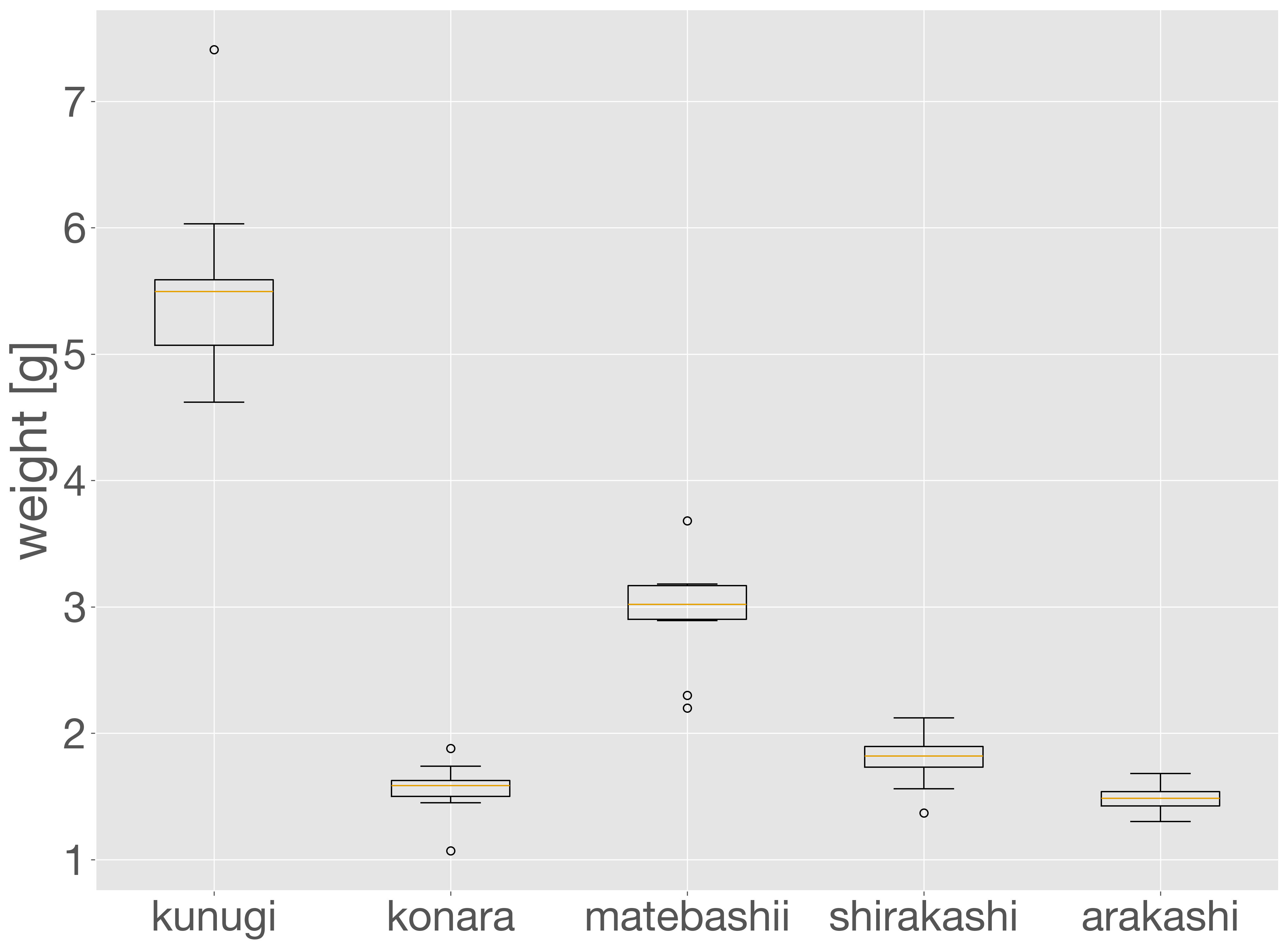
次に、樹種ごとにどんぐりの重さだけを抽出し、それぞれをリストに保存して、リストのリストとして boxplot に渡す方法を紹介します。これにより、どの樹種が重いどんぐりをつけるかといった傾向を比較できます。
x = []
y = []
for tree in acorn_data['tree'].unique():
x.append(tree)
y.append(acorn_data.loc[acorn_data['tree'] == tree, 'weight'])
fig = plt.figure()
ax = fig.add_subplot()
ax.boxplot(y, labels=x)
ax.set_ylabel('weight [g]')
plt.show()
7.2.6. バイオリンプロット#
バイオリンプロットは、ボックスプロットと同様に、複数のカテゴリにおける連続値データの分布を比較するためのグラフです。ボックスプロットが四分位点(中央値、第一・第三四分位数など)を強調するのに対し、バイオリンプロットではデータの分布の形(カーネル密度)を推定して可視化します。正規分布でないデータや、分布の形そのものを比較したい場合に、バイオリンプロットの方が有効です。
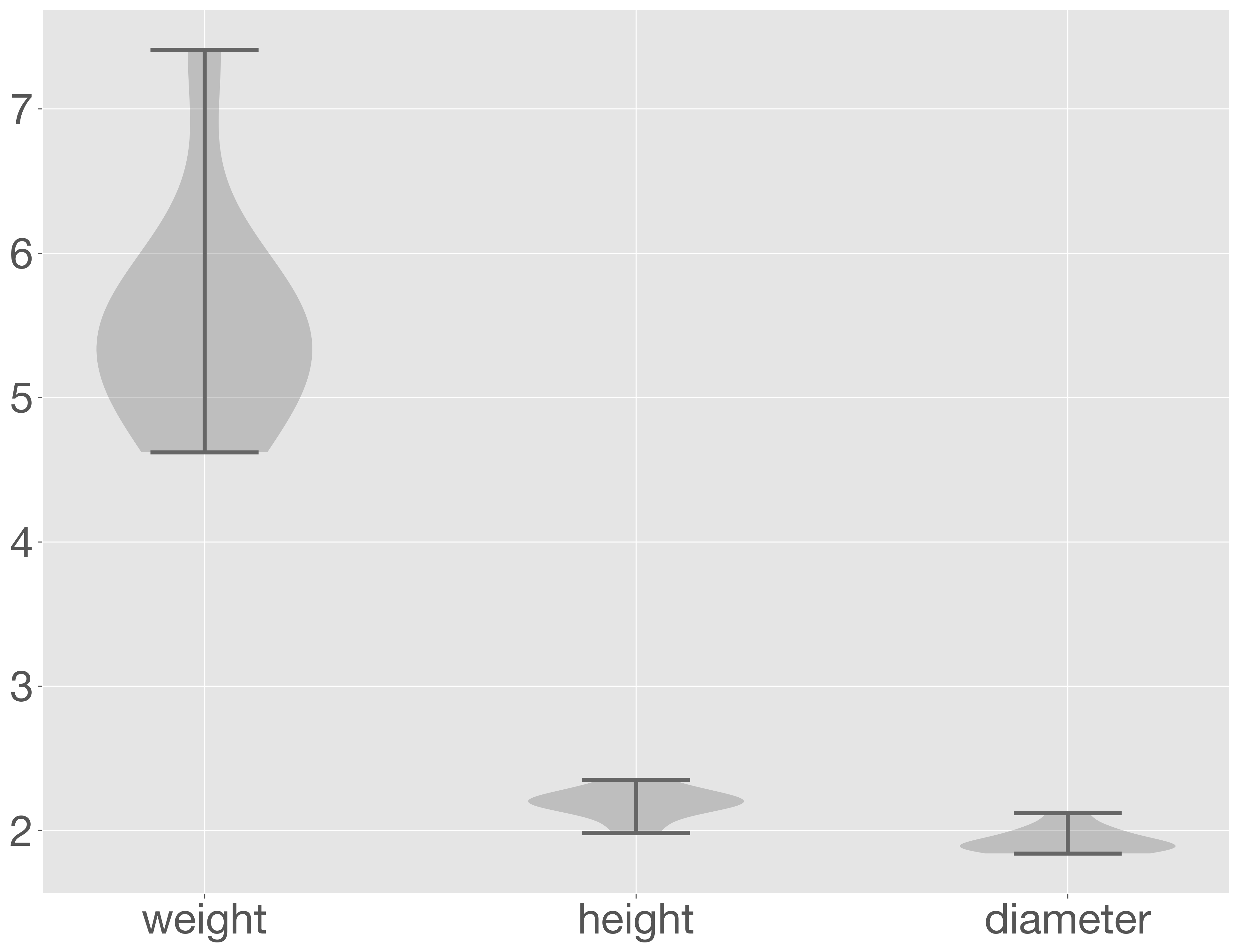
バイオリンプロットは violinplot メソッドを使って描きます。ただし、boxplot メソッドと異なり、violinplot には labels オプションがありません。そのため、プロットを描くと横軸のラベルは自動的に数値(1, 2, 3, …)になります。横軸を変数名などのわかりやすいラベルに変更するには、set_xticks を使って明示的に設定する必要があります。
kunugi = acorn_data.loc[acorn_data['tree'] == 'kunugi', :].iloc[:, 1:]
fig = plt.figure()
ax = fig.add_subplot()
ax.violinplot(kunugi)
ax.set_xticks(np.arange(1, 1 + len(kunugi.columns)))
ax.set_xticklabels(kunugi.columns)
plt.show()
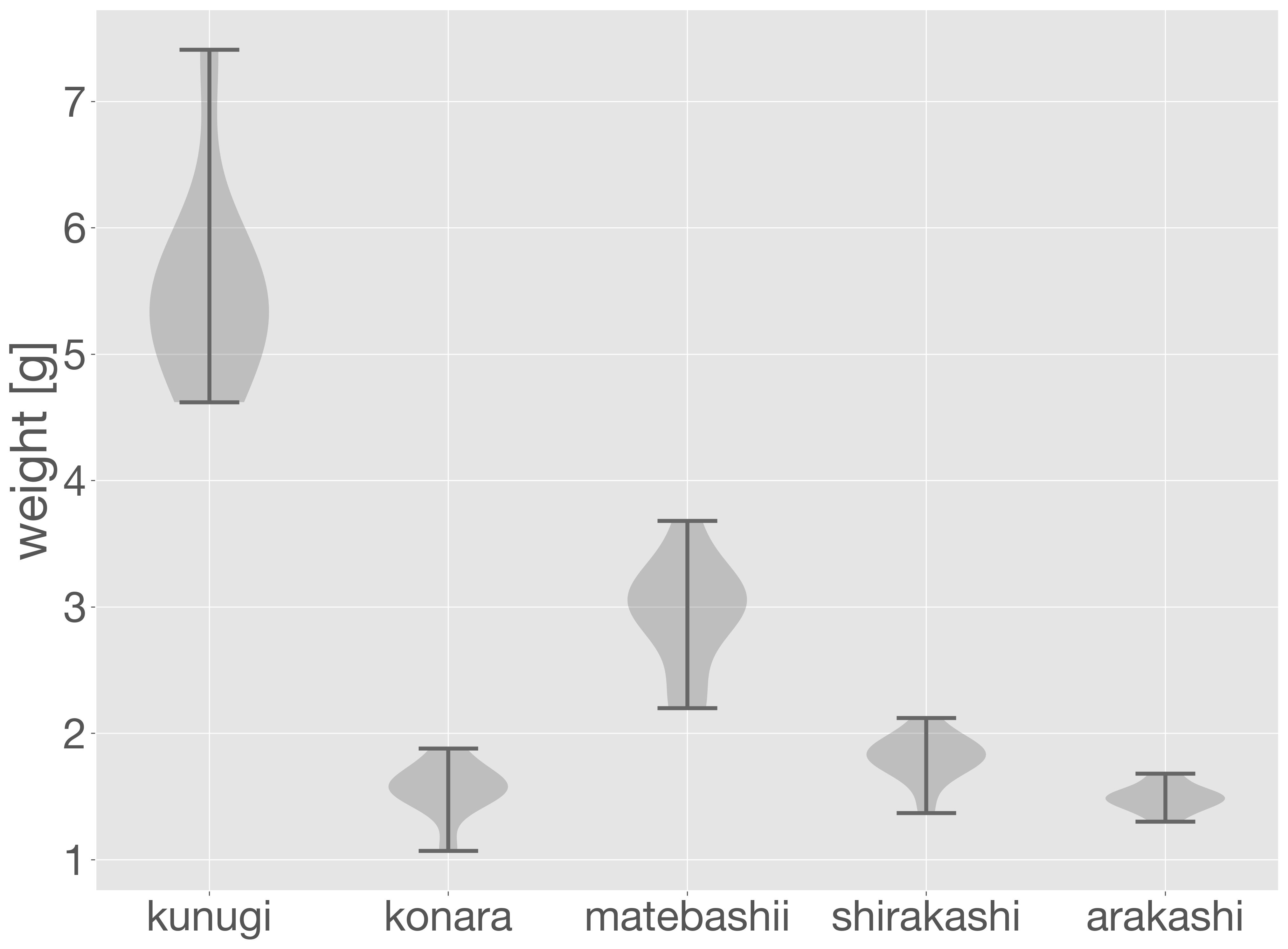
x = []
y = []
for tree in acorn_data['tree'].unique():
x.append(tree)
y.append(acorn_data.loc[acorn_data['tree'] == tree, 'weight'])
fig = plt.figure()
ax = fig.add_subplot()
ax.violinplot(y)
ax.set_xticks(np.arange(1, 1 + len(x)))
ax.set_xticklabels(x)
ax.set_ylabel('weight [g]')
plt.show()
7.2.7. ドットプロット#
ドットプロットは、1 つのデータ点を 1 つの点(ドット)で描画するグラフで、データそのものを可視化する方法です。カテゴリごとの個々のデータ値を点として表示するため、データのばらつきや分布の様子を視覚的に把握しやすくなります。
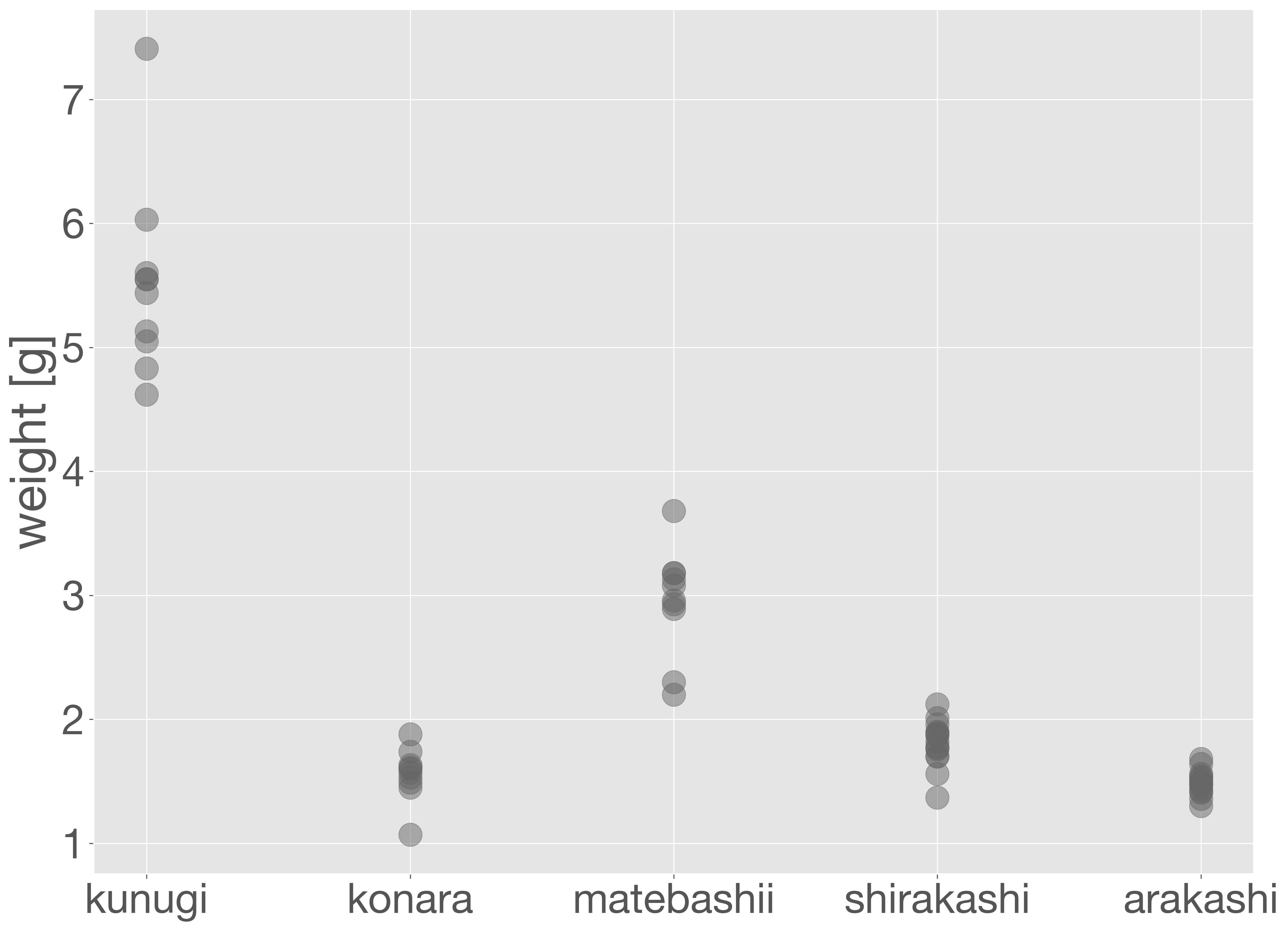
たとえば、各種のどんぐりの「重さ」をカテゴリごとにドットプロットで表示するには、以下のように scatter メソッドを使って描きます。
tree_id = {}
for i, tree in enumerate(acorn_data['tree'].unique()):
tree_id[tree] = i
x = acorn_data['tree'].replace(tree_id)
y = acorn_data['weight']
fig = plt.figure()
ax = fig.add_subplot()
ax.scatter(x, y, alpha = 0.5)
ax.set_xticks(np.arange(len(tree_id)))
ax.set_xticklabels(sorted(tree_id, key=tree_id.get))
ax.set_ylabel('weight [g]')
plt.show()
ドットプロットでは、同じか近い値のサンプルが多い場合に点が重なってしまい、分布がわかりにくくなります。そこで、横軸に小さな乱数を加えて点を左右にばらすことで、点同士の重なりを避けることができます。このようなグラフはジッタープロットと呼ばれています。なお、横軸はカテゴリであるため、多少位置をずらしても意味の解釈には影響しません。
tree_id = {}
for i, tree in enumerate(acorn_data['tree'].unique()):
tree_id[tree] = i
x = acorn_data['tree'].replace(tree_id)
x = x + np.random.uniform(-0.2, 0.2, len(x))
y = acorn_data['weight']
fig = plt.figure()
ax = fig.add_subplot()
ax.scatter(x, y, alpha = 0.5)
ax.set_xticks(np.arange(len(tree_id)))
ax.set_xticklabels(sorted(tree_id, key=tree_id.get))
ax.set_ylabel('weight [g]')
plt.show()
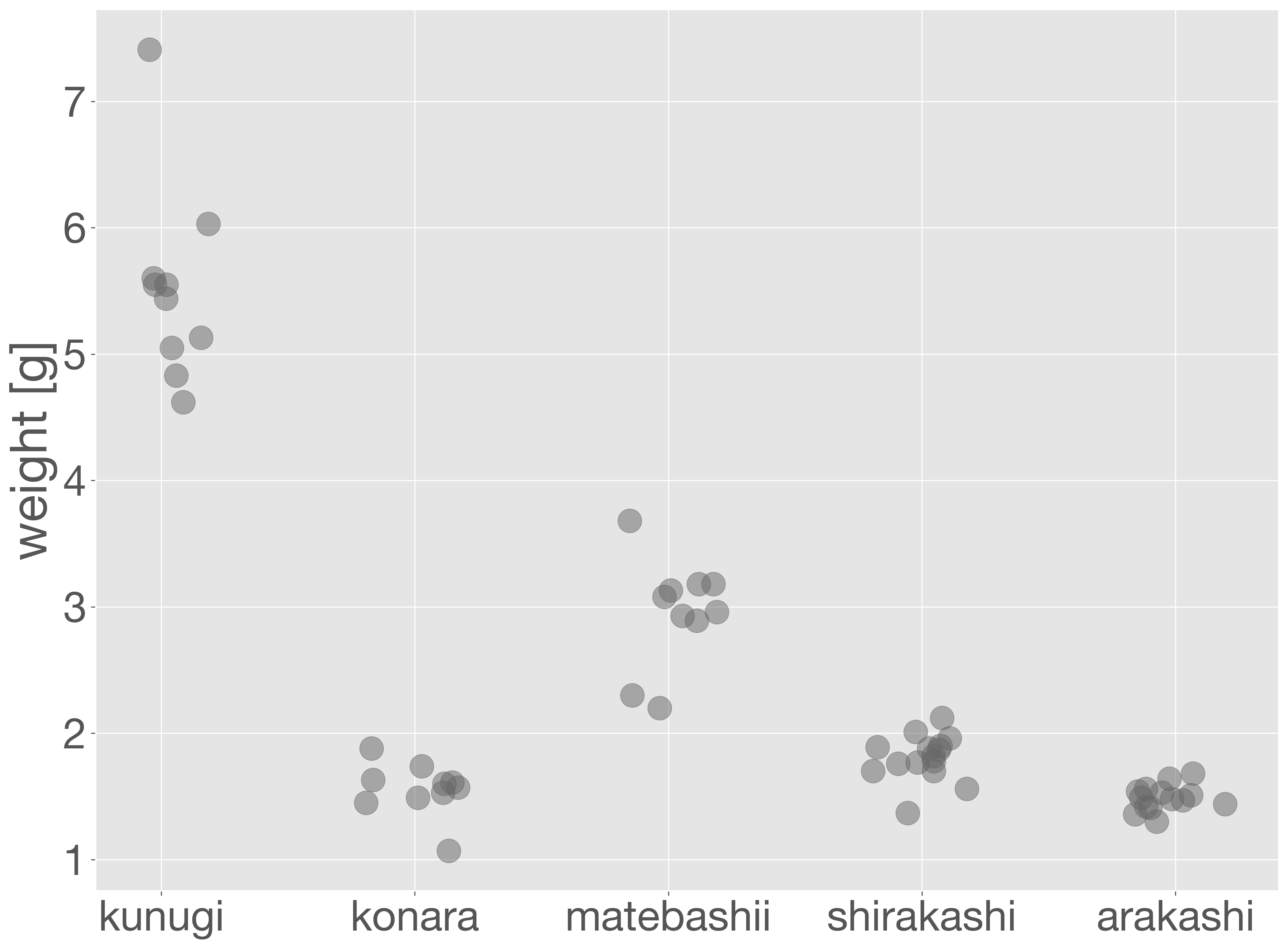
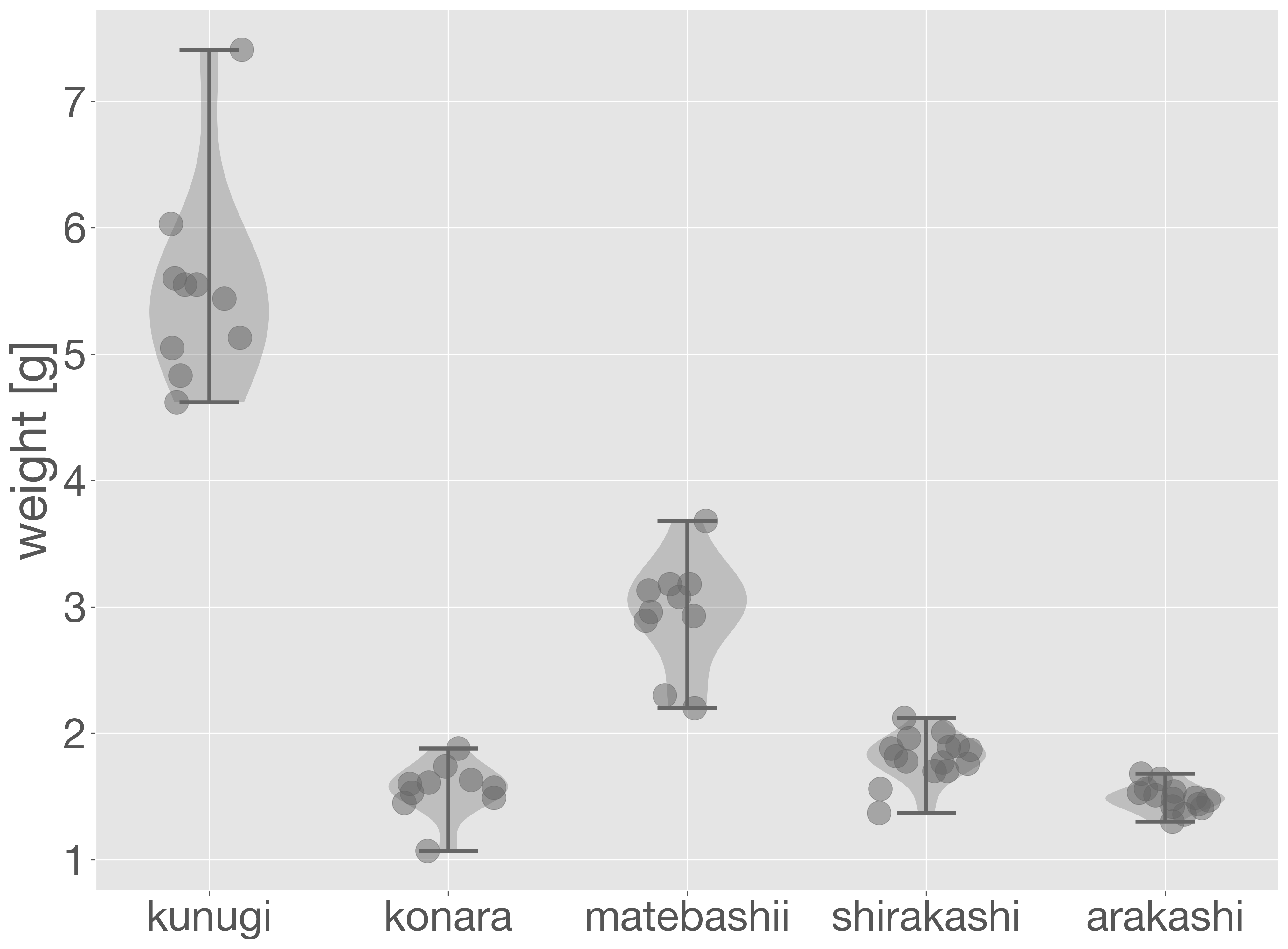
ジッタープロットは、単体でもデータの分布を可視化できますが、ボックスプロットやバイオリンプロットと重ねて表示することで、分布の概要と個々のデータ点の両方を視覚的に捉えることができ、より正確なデータの理解につながります。
tree_id = {}
x = []
y = []
for i, tree in enumerate(acorn_data['tree'].unique()):
x.append(tree)
y.append(acorn_data.loc[acorn_data['tree'] == tree, 'weight'])
tree_id[tree] = i + 1
acorn_data['x'] = acorn_data['tree'].replace(tree_id) + np.random.uniform(-0.2, 0.2, len(acorn_data['tree']))
fig = plt.figure()
ax = fig.add_subplot()
ax.violinplot(y)
ax.scatter(acorn_data['x'], acorn_data['weight'], alpha = 0.5)
ax.set_xticks(np.arange(1, 1 + len(x)))
ax.set_xticklabels(x)
ax.set_ylabel('weight [g]')
plt.show()