7.6. スパース回帰

7.6.1. 正則化

回帰分析や予測モデルを構築する際、サンプル数が説明変数の数より少ない場合や、説明変数同士に強い相関がある場合、通常の回帰モデルではパラメーターを安定的に推定できないことがあります。これらの問題に対処するために、正則化（regularization）と呼ばれる手法が用いられます。正則化では、パラメーターに制約条件を加えることで推定値を安定化させます。代表的な正則化手法には、L1 正則化（L1 regularization）と L2 正則化（L2 regularization）があります。

Pythonでは、statsmodels と scikit-learn の 2 つのライブラリを使用してスパース回帰を実行できます。scikit-learn は機械学習のモデルを作るためのアルゴリズムやハイパーパラメーターを自動的に決めてくれる機械学習を効率進める機構が実装されています。そのため、ここでは、ハイパーパラメーターの調整が容易な scikit-learnを利用してスパース回帰を解説します。

7.6.2. L1 正則化

3 つの説明変数からなるモデル \(y = \beta_0 + \beta_1x_1 + \beta_2x_2 + \beta_3x_3\) を考えます。L1 正則化では、次の制約条件をパラメーターに課します。

\[ |\beta_1| + |\beta_2| + |\beta_3| \leq \alpha \]

このとき、\(\alpha\) の値を適切に小さくしていくと、この条件制約条件を満たすために、一部の \(\beta\) が 0 にならなくてはなりません。これにより、目的変数に影響を与えない説明変数の係数が 0 となり、実質、モデルに組み込まれなくなります。この性質により、L1 正則化を利用した回帰は、変数選択とモデル構築を同時に行います。この手法は LASSO（Least Absolute Shrinkage and Selection Operator）として知られています。

説明変数が多いデータを用いて、Pythonのライブラリ scikit-learn を使った LASSO 回帰を実施してみましょう。今回は、UC Irvine Machine Learning Repository から提供されているアワビのデータを使用します。このデータセットには、アワビの年齢（目的変数）と、アワビのさまざまなサイズや重さ（説明変数）が含まれています。

# !wget https://py.biopapyrus.jp/data/abalone.csv

abalone = pd.read_csv('abalone.csv', header=0, comment='#')
abalone.head()

	Sex	Length	Diameter	Height	WholeWeight	ShuckedWeight	VisceraWeight	ShellWeight	Rings
0	M	0.455	0.365	0.095	0.5140	0.2245	0.1010	0.150	15
1	M	0.350	0.265	0.090	0.2255	0.0995	0.0485	0.070	7
2	F	0.530	0.420	0.135	0.6770	0.2565	0.1415	0.210	9
3	M	0.440	0.365	0.125	0.5160	0.2155	0.1140	0.155	10
4	I	0.330	0.255	0.080	0.2050	0.0895	0.0395	0.055	7

性別に関するデータはカテゴリ変数であり、今回の回帰分析では使用しません。また、説明変数をすべて標準化します。これは、LASSO が変数のスケールに敏感であるため、推定される係数が適切に比較可能になるようにするためです。

X = abalone.iloc[:, 1:8]
X = (X - X.mean()) / X.std()
y = abalone.iloc[:, 8]

LASSO 回帰では、\(\alpha\)（正則化強度）を事前に決定する必要があります。解析者が特定の値を 1 つ決めて解析を進めることも可能だが、解析者が決めた値が最適な値であると保証がありません。したがって、いくつかの候補を用意し、最適な \(\alpha\) を選定します。

たとえば、\(\alpha = 0.001,\ 0.01,\ 0.1,\ 1,\ 10,\ 100\) といったように、複数の候補を用意します。次に、解析に使用するデータセットを 学習用サブセット（トレーニングデータ）と 検証用サブセット（バリデーションデータ）に分割します。そして、学習用サブセットを用いて、それぞれの \(\alpha\) の候補に対してモデルを構築します。その後、構築した各モデルに対して検証用サブセットを入力し、予測精度や誤差を計算します。この評価結果をもとに、誤差が最も小さいモデルに対応する \(\alpha\) を最適な値として選択します。このように、解析者が事前に設定するパラメーターのことを、ハイパーパラメーター（hyperparameter）と呼びます。スパース回帰では、罰則の強さを調整するハイパーパラメーターを最適化する必要があるため、従来の統計手法よりも機械学習のアプローチに近い側面を持ちます。

Note

1 つのデータセットをいくつかのサブセットに分割し、それらを使ってモデルの構築と検証を繰り返すことで、最適なモデルやハイパーパラメーターを選択する手法は、交差検証（cross validation）と呼ばれます。

ここで \(\alpha\) の候補を作ります。

alphas = 10 ** np.arange(-6, 2, 0.1)
alphas

array([1.00000000e-06, 1.25892541e-06, 1.58489319e-06, 1.99526231e-06,
       2.51188643e-06, 3.16227766e-06, 3.98107171e-06, 5.01187234e-06,
       6.30957344e-06, 7.94328235e-06, 1.00000000e-05, 1.25892541e-05,
       1.58489319e-05, 1.99526231e-05, 2.51188643e-05, 3.16227766e-05,
       3.98107171e-05, 5.01187234e-05, 6.30957344e-05, 7.94328235e-05,
       1.00000000e-04, 1.25892541e-04, 1.58489319e-04, 1.99526231e-04,
       2.51188643e-04, 3.16227766e-04, 3.98107171e-04, 5.01187234e-04,
       6.30957344e-04, 7.94328235e-04, 1.00000000e-03, 1.25892541e-03,
       1.58489319e-03, 1.99526231e-03, 2.51188643e-03, 3.16227766e-03,
       3.98107171e-03, 5.01187234e-03, 6.30957344e-03, 7.94328235e-03,
       1.00000000e-02, 1.25892541e-02, 1.58489319e-02, 1.99526231e-02,
       2.51188643e-02, 3.16227766e-02, 3.98107171e-02, 5.01187234e-02,
       6.30957344e-02, 7.94328235e-02, 1.00000000e-01, 1.25892541e-01,
       1.58489319e-01, 1.99526231e-01, 2.51188643e-01, 3.16227766e-01,
       3.98107171e-01, 5.01187234e-01, 6.30957344e-01, 7.94328235e-01,
       1.00000000e+00, 1.25892541e+00, 1.58489319e+00, 1.99526231e+00,
       2.51188643e+00, 3.16227766e+00, 3.98107171e+00, 5.01187234e+00,
       6.30957344e+00, 7.94328235e+00, 1.00000000e+01, 1.25892541e+01,
       1.58489319e+01, 1.99526231e+01, 2.51188643e+01, 3.16227766e+01,
       3.98107171e+01, 5.01187234e+01, 6.30957344e+01, 7.94328235e+01])

次にこれらの \(\alpha\) の候補の中から最適な \(\alpha\) を決めていきます。データセットを 2 つのサブセットに分けて、片方でモデルを作り、もう片方で検証することも可能です。しかし、データセットを 2 つのサブセットにわけるとき、たまたまデータが不均一に分けられる可能性があります。そこで、データセットを 5 のサブセットに分けて、これらのサブセットを適切に組み合わせてモデルの構築と検証を繰り返していきます。これにより、データ分割の偏りを減らし、より安定した評価が可能です。

from sklearn.linear_model import Lasso
from sklearn.model_selection import GridSearchCV

parmas = {'alpha': alphas}

gs = GridSearchCV(Lasso(), parmas, cv=5)
gs.fit(X, y)

最適な \(\alpha\) は、次のようにして取得できます。

best_param = gs.best_params_
best_param

{'alpha': np.float64(0.007943282347242562)}

最適な \(\alpha\) に対応する最適なモデルも同時に構築されます。このモデルは線形回帰モデルであるため、それぞれの説明変数には係数が割り当てられます。各説明変数に対応する係数は、次のように取得できます。なお、係数が 0 になっている説明変数は、LASSO によってその変数がアワビの年齢を説明するうえで重要でないと判断され、モデルに組み込まれなかったことを意味します。

best_model = gs.best_estimator_
best_model.coef_

array([ 0.        ,  1.10457845,  0.48829149,  3.39687841, -3.97048191,
       -0.72846545,  1.53673772])

\(\alpha\) を変化させたときの各変数の係数の変化を解パス（solution path）として可視化することができます。次のコードを実行すると、解パスがプロットされます。

lasso = Lasso()
coefs = []

for a in alphas:
    lasso.set_params(alpha=a)
    lasso.fit(X, y)
    coefs.append(lasso.coef_)

fig = plt.figure()
ax = fig.add_subplot()
for i in range(X.shape[1]):
    ax.plot(alphas, [coef[i] for coef in coefs], label=X.columns[i])
ax.vlines(best_param['alpha'], -5, 5, colors='#666666', linestyles='dashed')
ax.set_xscale('log')
ax.legend()
ax.set_xlabel('alpha')
ax.set_ylabel('Standardized Coefficients')
plt.show()

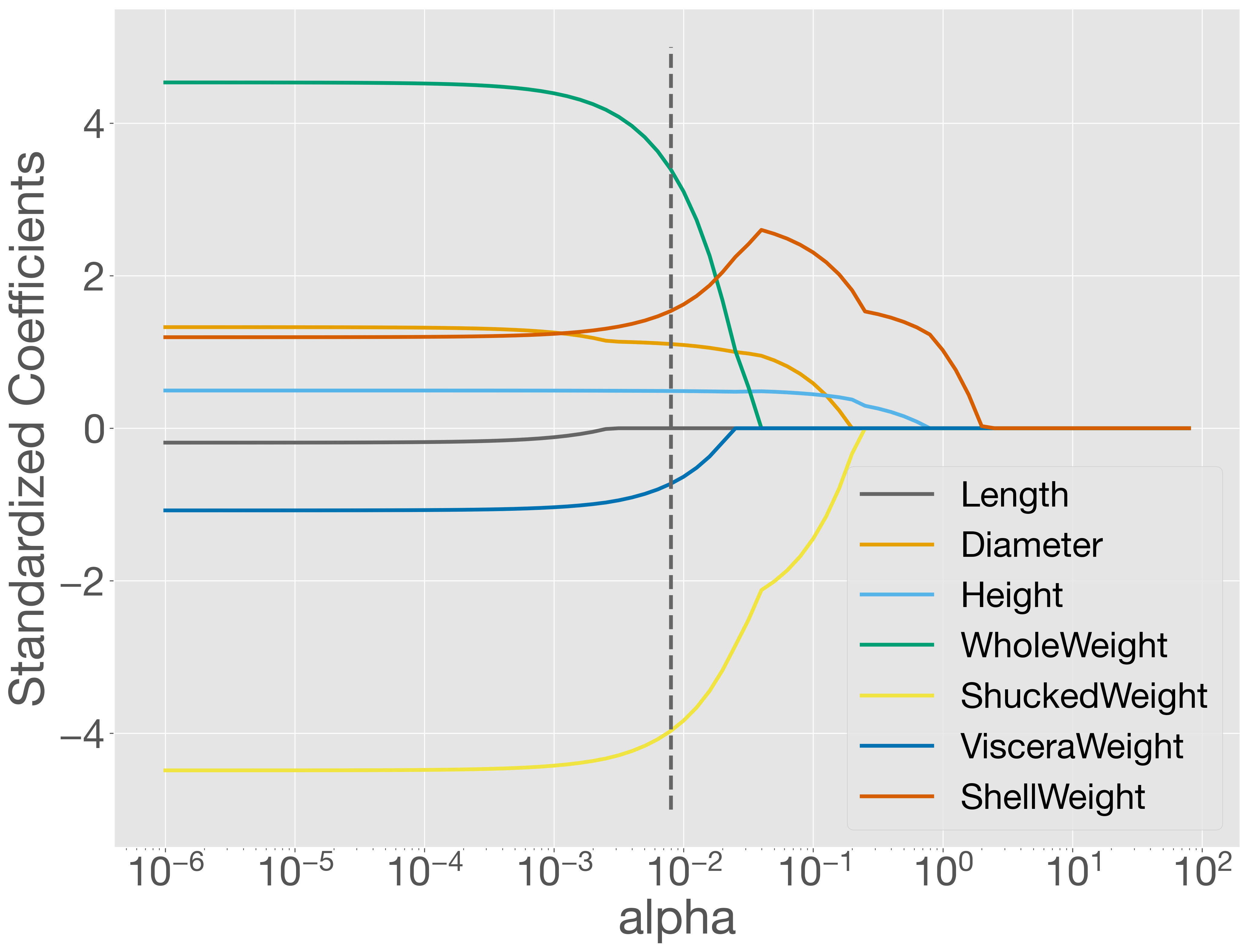
このプロットを見ると、正則化パラメーター \(\alpha\) が大きくなるにつれて、多くの係数が 0 に近づき、最終的には 0 になることがわかります。点線で示された最適な \(\alpha\) の位置では、Length の係数のみが 0 になっており、これは best_model.coef_ の出力結果とも一致しています。

予測に重点を置いた機械学習モデルを構築する場合、LASSO によってモデルを作成した後に、テストデータを用いて予測性能を評価することが重要です。そのためには、データを学習用、検証用、テスト用のサブセットに適切に分割する必要があります。また、説明変数のスケールをそろえるために正規化を行う場合は、scikit-learn の StandardScaler を用いると便利です。さらに、StandardScaler と LASSO をパイプラインとしてまとめ、ハイパーパラメーターの探索まで一貫して実施すると、より効率的な分析が可能になります。ここではその詳細を割愛します。

正直に言うと、細かい話を始めた瞬間、読者が「もういいや」と消えていくのが目に見えているので、この辺りで止めます。

7.6.3. L2 正則化

L2 正則化では、次の制約条件をパラメーターに課します。

\[ \beta_1^2 + \beta_2^2 + \cdots + \beta_n^2 \leq \alpha \]

L2 正則化では、\(\alpha\) を小さくすると、すべてのパラメーターが均一に小さくなるよう調整されます。これは、値の小さいパラメーターをゼロにするよりも、値の大きいパラメーターを小さくした方が二乗の効果で式全体がより小さくなりやすいためです。このように、L2 正則化を用いた回帰はパラメーターがゼロになることは少ないものの、サンプル数が少ない場合や説明変数同士に強い相関がある場合でも、安定したモデルを構築することが可能です。

L2 正則化の制約条件は、すべてのパラメーターの二乗和をある値以下に抑えるものなので、パラメーター空間では球面や楕円体の内部に値を収めることに相当します。この形状が「尾根（ridge）」や「稜線」に例えられます。この手法は Hoerl と Kennard によって提案され、従来の最小二乗法回帰（ordinary least squares regression）に ridge-like な制約を加えることからRidge 回帰（Ridge regresion）と呼ばれるようになりました。

from sklearn.linear_model import Ridge
from sklearn.model_selection import GridSearchCV

parmas = {'alpha': 10 ** np.arange(-6, 2, 0.1)}

gs = GridSearchCV(Ridge(), parmas, cv=5)
gs.fit(X, y)
best_param = gs.best_params_
best_model = gs.best_estimator_

best_param

{'alpha': np.float64(9.999999999999428)}

best_model.coef_

array([-0.109815  ,  1.22817746,  0.50371486,  3.32882412, -3.90295352,
       -0.80040285,  1.58567211])

7.6.3.1. Elastic Net

L1 正規化と L2 正規化をバランスよく組み合わせて（elastic）、多数の説明変数がある中で、効果的に重要な変数を選択しつつ、全体の関係性を網羅的に（net）回帰する方法もあります。これを Elastic Net と呼びます。Elastic Net では、次の制約条件を使用します。

\[ \lambda (|\beta_1| + |\beta_2| + \cdots) + (1 - \lambda) (\beta_1^2 + \beta_2^2 + \cdots) \leq \alpha \]

ここで、\(\lambda\) は L1 正則化と L2 正則化のバランスを調整するためのパラメーターです。Elastic Net に対して、2 つのハイパーパラメーターを適切に設定する必要があります。この際も、GridSearchCV 関数を利用すれば、あらかじめ指定した複数の候補値に対して、すべての組み合わせを試行し、その中から最も予測性能の高いハイパーパラメーターの組み合わせを自動的に選択してくれます。

from sklearn.linear_model import ElasticNet
from sklearn.model_selection import GridSearchCV

parmas = {'alpha': 10 ** np.arange(-6, 2, 0.1),
          'l1_ratio': np.arange(0, 1, 0.1)}


gs = GridSearchCV(ElasticNet(), parmas, cv=5)
gs.fit(X, y)
best_param = gs.best_params_
best_model = gs.best_estimator_

best_param

{'alpha': np.float64(0.0031622776601682888), 'l1_ratio': np.float64(0.0)}

best_model.coef_

array([-0.08820615,  1.20185035,  0.50631828,  3.06670063, -3.77062051,
       -0.74101129,  1.66622198])